Chapitre XIV – Lois Normales 1 Approximation de la loi binomiale

Chapitre XIV – Lois Normales
1 Approximation de la loi binomiale centrée réduire
Théorème 1. (de Moivre-Laplace)
Pour tout entier naturel n, soit Xnune variable aléatoire qui suit une loi binomiale B(n;p).
On pose Zn=Xn−n p
n p (1 −p)
p,variable centrée réduite associée à Xn(elle a pour espérance 0 et pour écart-type 1).
Pour tous réels a, b tels que a < b :lim
n→+∞
P(a6Zn6b) = Za
b1
2π
√e−x2
2dx
Remarque. Quand n>30 ; n p >5et n p (1 −p)>5, on pourra approcher une loi binomiale B(n;p)par une loi normale N(µ;σ2)avec
µ=n p et σ=n p (1 −p)avec une erreur très faible sur les probabilités calculées.
2 Loi normale centrée réduite : N(0; 1)
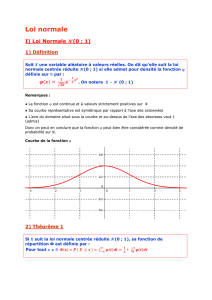
Définition 1. On dit qu’une variable aléatoire continue Xsuit la loi normale centrée réduite, notée N(0; 1), si elle admet comme
densité de probabilité la fonction ϕ, définie sur Rpar :
ϕ(x) = 1
2π
√e−
x2
2
ϕest appelée fonction de densité de Laplace-Gauss.
Remarque. •Si Xest une variable aléatoire qui suit la loi normale N(0; 1) alors, pour tous réels a, b tels que a < b :
P(a6X6b) = Za
b1
2π
√e−
x2
2dx
•On calculera P(a6X6b)à la calculatrice ou à l’aide d’une table de valeurs.
Proposition 1. Soit Xune variable aléatoire qui suit la loi normale,N(0; 1).
L’espérance de X,E(X) = 0 (la loi est centrée en 0) et l’écart-type σ(X) = 1 (la loi est réduite).
Proposition 2. Fonction de densité ϕet courbe de Gauss
1. ϕest une fonction de densité dont la courbe est appelée courbe de Gauss ou gaussienne.
•ϕest continue et positive sur R,
•Z−∞
+∞ϕ(x) dx=Z−∞
+∞1
2π
√e−x2
2dx= 1 (aire totale sous la courbe).
2. Sa courbe est symétrique par rapport à l’axe des ordonnées (ϕpaire), elle a pour maximum ϕ(0) = 1
2π
√≈0,4.
3. Pour tout réel a,
0
0,5 0,5
0
−aa
0
a
P(X60) = P(X>0) = 1
2P(X>a) = P(X6−a)P(X6a) = 1 −P(X > a)
À connaître. Soit Xune variable aléatoire qui suit la loi normale,N(0; 1).
0
−11
0,68
P(−16X61) ≈0,68
0
−22
0,95
P(−26X62) ≈0,95
0
−33
0,997
P(−36X63) ≈0,997
À la calculatrice. Soit Xune variable aléatoire qui suit la loi normale,N(0; 1), pour calculer P(a6X6b):
On connaît [a;b]et on veut déterminer une probabilité.
TI
Touches 2nde +var (donne distr )
normalFRép(a,b,µ,σ)
Casio
Touches MENU Stat DIST Norm NCD
Lower : a Upper : b σ: 1 µ: 0
En prenant pour valeurs de aet bdes réels, -10^99 (pour −∞) ou 10^99 (pour +∞)

Intervalle centré de probabilité donnée
Proposition 3. Si Xest une variable aléatoire qui suit la loi normale,N(0; 1) alors pour tout réel α∈]0; 1[, il existe uα>0tel que :
P(−uα6X6uα) = 1 −α
Démonstration. ROC dans le cahier de bord 
À connaître. Soit Xune variable aléatoire qui suit la loi normale,N(0; 1).
Pour α= 0,05,1−α= 0,95 et u0,05 ≈1,96 Pour α= 0,01,1−α= 0,99 et u0,01 ≈2,58
0
−1,96 1,96
0,95
0
−2,58 2,58
0,99
P(−1,96 6X61,96)≈0,95 P(−2,58 6X62,58)≈0,99
À la calculatrice. Si Xsuit la loi normale,N(0; 1). Pour calculer la valeur de a telle que P(X6a) = 0,4 par exemple.
On connaît une probabilité et on veut déteminer un intervalle ]−∞;a].
TI
Touches 2nde +var (donne distr )
FracNormal(p,µ,σ)avec p=0.4,µ=1,σ=1
Casio
Touches MENU Stat DIST Norm InvN
Area : 0.4 σ: 1 µ: 1
3 Loi normale d’espérance µet d’écart-type σ:N(µ;σ2)
Définition 2. On dit qu’une variable aléatoire continue Xsuit la loi normale de paramètres µet σ, notée N(µ;σ2), si la variable
aléatoire Y=X−µ
σsuit une loi centrée réduite N(0; 1).
Représentation graphique.
→La fonction de densité de la loi N(µ;σ2)n’est pas à connaître. Sa
courbe est appelée courbe de Gauss ou gaussienne.
→Elle est symétrique par rapport à la droite d’équation x=µ.
On a ci-contre les courbes des densités des lois normales :
N(0; 12);N(2; 12);N(7; 12).
→L’écart-type σdonne la « dispersion » autour de la moyenne. Plus
σest grand, plus le sommet de la courbe est bas.
On a ci-contre les courbes des densités des lois normales :
N(2; 0,52);N(2; 12);N(2; 22).
Interprétation.
Xa pour moyenne µet écart-type σ
X−µest centrée, elle a pour moyenne 0et écart-type σ
Y=X−µ
σest centrée et réduite, elle a pour moyenne 0et écart-type 1
0 1 2 3 4 5 6 7 8 9−1−2−3−4
0
0.2
0.4
µ= 0 µ= 2 µ= 7
0 1 2 3 4 5 6 7−1−2−3−4
0
0.2
0.4
0.6
0.8σ= 0,5
σ= 1
σ= 2
Proposition 4. Soit Xune variable aléatoire qui suit la loi normale,N(µ;σ2).
L’espérance de X,E(X) = µet l’écart-type σ(X) = σ.
Propriété 1. Pour tout réel a,
µ
0,5 0,5
µ
µ−a µ +a
a
P(X6µ) = P(X>µ) = 0,5 P(X6µ−a) = P(X>µ+a)P(X6a) = 1 −P(X>a)
Tale S2 Chapitre XIV – Lois Normales Guist’hau - 2014/2015
2

À connaître. Soit Xune variable aléatoire qui suit la loi normale,N(µ;σ2).
µ
µ−σ µ +σ
0,68
P(µ−σ6X6µ+σ)≈0,68
µ
µ−2σ µ + 2σ
0,95
P(µ−2σ6X6µ+ 2 σ)≈0,95
µ
µ−3σ µ + 3σ
0,997
P(µ−3σ6X6µ+ 3 σ)≈0,997
Exemple 1. Soit Xla variable aléatoire égale au temps de travail personnel quotidien d’un élève de terminale. Xsuit approximativement une loi normale
de moyenne µ= 3 et σ= 0,9. Déterminer P(2,1 6X63,9) et P(1,2 6X64,8).
P(2,1 6X63,9) = P(3 −0,9 6X63 + 0,9) ≈0,68 P(1,2 6X64,8) = P(3 −2×0,9 6X63 + 2 ×0,9) ≈0,95
À la calculatrice. On reprend les mêmes commandes que pour la loi N(0; 1).
Exemple 2. Soit Xla variable aléatoire égale au temps de travail personnel quotidien d’un élève de terminale (en heures). Xsuit approximativement une
loi normale de moyenne µ= 3 et σ= 0,9.
•Calculer P(1 6X65) et P(X < 4) puis en déduire P(X>5) et P(4 6X < 5). Donner les résultats à 10−4près.
TI
Touches 2nde +var (donne distr )
normalFRép(a,b,µ,σ)
ici normalFRép(1,5,3,0.9)
Casio
Touches MENU Stat DIST Norm NCD
Lower : 1
Upper : 5
σ: 0.9
µ: 3
◦À la calculatrice :
P(1 6X65) ≈0,9737
P(X > 4) ≈0,1333 à la calculatrice, P(X > 4) ≈P(4 < X < 1099)
Interprétation :
La probabilité qu’un élève travaille entre 1 et 5 heures est de 0,97 environ.
Environ 13 % des élèves travaillent plus de 4 heures par jour.
◦P(X>5) = 0,5 −P(3 6X65)
P(X>5) = 0,5 −P(1 6X65)
2
P(X>5) ≈0,5 −0,9737
2
P(X>5) ≈0,5 −0,4869
P(X>5) ≈0,0131 à la calculatrice, P(5 6X < 1099)≈0,1201
3
1 5
◦P(3 < X < 4) = 0,5 −P(X > 4) ≈0,5 −0,1333 = 0,3667
donc P(4 6X < 5) = P(3 6X65) −P(3 < X < 4)
P(4 6X < 5) = P(1 6X65)
2−P(3 < X < 4)
P(4 6X < 5) = 0,9737
2−0,3667
P(4 6X < 5) = 0,1202 à la calculatrice, P(4 6X < 5) ≈0,1201
3
1 54
•Calculer la valeur de atelle que P(X6a) = 0,40 et la valeur de btelle que P(X > b) = 0,2
TI
Touches 2nde +var (donne distr )
FracNormal(p,µ,σ)
ici FracNormal(0.4,3,0.9) donne 2.7720
Casio
Touches MENU Stat DIST Norm InvN
Area : 0.4
σ: 0.9
µ: 3
◦P(X6a) = 0,40 pour a≈2,7720
◦P(X > b) = 0,2 P(X < b) = 0,8 pour b≈3,7574
•Déterminer un intervalle Ide centre µtel que P(X∈I) = 0,70
Soit a > 0tel que I= [3 −a; 3 + a]
On cherche a > 0tel que : P(3 −a < X < 3 + a) = 0,70
P(3 −a < X < 3) = 0,35
P(X < 3−a) = 0,15
c’est-à-dire pour 3−a≈2,0672 soit a= 0,9328
On en déduit que I= [2,0672; 3,9328]
3
3−a3 + a
Tale S2 Chapitre XIV – Lois Normales Guist’hau - 2014/2015
3

Exemple 3. Soit Xune variable aléatoire suivant la loi normale, de moyenne µ=20 (et d’écart-type σ) :
20
0,5 0,5
P(X620) = 0,5 et P(X>20) = 0,5
20
20 −9 20 + 9
P(X620 −9) = P(X>20 + 9)
10
P(X610) = 1 −P(X>10)
0
0,5 0,5
0
−aa
0
a
0 1 2 3−1−2−3−4
0
0.4
Cφ
0 1 2 3 4 5 6 7 8 9 10 11−1−2−3−4
0
µ= 0 µ= 2 µ= 7
0 1 2 3 4 5 6 7−1−2−3−4
0
0.2
0.4
0.6
0.8σ= 0,5
σ= 1
σ= 2
Interprétation.
Xa pour moyenne µet écart-type σ
X−µest centrée, elle a pour moyenne 0et écart-type σ
Y=X−µ
σest centrée et réduite, elle a pour moyenne 0et écart-type 1
TI
Touche math
((6*X-Xš)/36,X,4,6) donne 0.2593
Casio
Touches MENU Stat DIST Norm NCD
Lower : 1
Tale S2 Chapitre XIV – Lois Normales Guist’hau - 2014/2015
4

Propriété 2. Soit Xune variable aléatoire qui suit la loi normale centrée réduite N(0; 1) et aet bdeux réels. Alors
P(X60) = 0,5 et P(X>0) = 0,5
P(X∈R) = 1
P(X6a) = 1 −P(X>a)
ou P(X6a) + P(X>a) = 1
P(X>b) = P(X6−b)
Tale S2 Chapitre XIV – Lois Normales Guist’hau - 2014/2015
5