Chapitre PARALLÉLOGRAMMES

Chapitre PARALLÉLOGRAMMES
 Figure obtenue à partir de la symétrie centrale
 Définition et propriétés découlant de celles de la symétrie centrale.
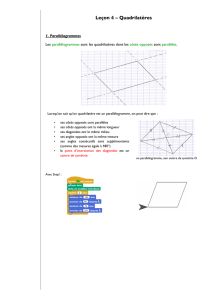
 Construction de parallélogrammes
 Premiers pas vers la démonstration : relier logiquement des "morceaux"
de raisonnement puis créer un raisonnement.
 Aire du parallélogramme
 Centre et axes de symétrie des figures
Remarques :
 Les propriétés sur les angles seront abordées dans le chapitre (10)
« Angles et parallélisme » après le chapitre (8) « Angles » étudié en
Grcom.
 La propriété « si un parallélogramme possède un angle droit alors c’est
un rectangle » pourrait être étudiée dans ce chapitre ( en utilisant la
propriété de 6
ème
, « si deux droites sont parallèles alors toute
perpendiculaire à l’une est perpendiculaire à l’autre ») mais le chapitre
est déjà assez long et la démonstration utilisant les angles est plus
naturelle…voir chapitre 10.

Chapitre PARALLÉLOGRAMME
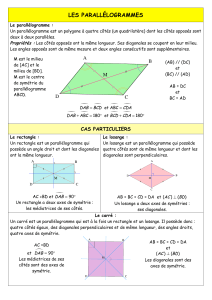
1) Parallélogramme :
Définition :
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles deux à deux.
Exemple :
ABCD est un parallélogramme signifie que
(AB) est parallèle à (CD) et (AD) est parallèle à (BC).
Remarques :
Dans la définition, on devrait écrire en toute rigueur, « les droites portant les côtés opposés sont
parallèles » mais pour alléger la rédaction, on se permet d'écrire « les côtés opposés sont parallèles ».
On pourra donc écrire « [AB] est parallèle à [CD] » et « [AD] est parallèle à [BC] ».
2) Parallélogramme et symétrie centrale :
a) Centre de symétrie d'une figure :
Lorsque le symétrique d'une figure par rapport à un point est elle même,
on dit que ce point est "le centre de symétrie" de la figure.
Exemples :
Remarque :
Si une figure a un centre de symétrie alors en la faisant tourner de 180° (demi-tour) autour de son centre
de symétrie, on obtient la même figure.
b) Centre de symétrie d'un parallélogramme : (propriété admise)
Si un quadrilatère est un parallélogramme
alors il possède un centre de symétrie qui est le point d'intersection de ses diagonales.
Exemple :
On dit que "O est le centre de symétrie du parallélogramme".
O est le point d'intersection des diagonales [DB] et [UE].
Le symétrique de D par rapport à O est B.
Le symétrique de U par rapport à O est E.
En faisant tourner de 180° le parallélogramme autour du point O,
on obtient le même parallélogramme.
centre de symétrie
B
D
A
C
O
U
E
D
B
centre de symétrie

3) Propriétés du parallélogramme :
a) Propriétés sur les diagonales d'un parallélogramme :
Si un quadrilatère est un parallélogramme alors ses diagonales se coupent en leur milieu.
Exemple :
VERT est un parallélogramme
donc le point O est le milieu des diagonales [VR] et [TE].
Démonstration :
Hypothèse :
VERT est un parallélogramme donc O est le centre de symétrie du parallélogramme VERT d'après le 2 b)
du cours.
Conclusions :
Le symétrique de V part rapport à O est R donc O est le milieu de [VR].
Le symétrique de E part rapport à O est T donc O est le milieu de [ET].
Remarque : Cette propriété permet de prouver qu'un point est le milieu d'un segment.
On a réciproquement :
Si un quadrilatère a ses diagonales qui se coupent en leur milieu
alors ce quadrilatère est un parallélogramme.
Démonstration :
Hypothèse :
O est le milieu de [VR] et O est le milieu de [ET].
Conclusions :
Le symétrique de V part rapport à O est R.
Le symétrique de E part rapport à O est T .
Le symétrique de (VE) est (RT) donc (VE)//(RT) ( le symétrique d'une droite est une droite parallèle).
Le symétrique de (VT) est (RE) donc (VT)//(RE).
VERT est un quadrilatère dont les côtés opposés sont parallèles 2 à 2 donc VERT est un parallélogramme.
b) Propriétés sur les longueurs des côtés d'un parallélogramme :
Si un quadrilatère est un parallélogramme
alors ses côtés opposés ont la même longueur.
Exemple :
CHUT est un parallélogramme donc CH=TU et CT=HU.
Démonstration :
Hypothèse :
CHUT est un parallélogramme donc il possède un centre de symétrie O
qui est le milieu de [CU] et [HT].
Conclusions :
Le symétrique de [CH] par rapport à O est [UT] donc CH=UT puisque la symétrie centrale conserve les
longueurs. De même on montre que CT=HU.
Remarque : Cette propriété permet de prouver que des segments ont la même longueur.
V E
R
T
O
C H
U
T
O
C H
U
T

On a réciproquement : (propriété admise)
Si un quadrilatère non croisé a ses côtés opposés qui ont la même longueur deux à deux
alors ce quadrilatère est un parallélogramme.
Exemple :
Dans le quadrilatère non croisé CHUT on a
CH=TU et CT=HU donc CHUT est un parallélogramme.
Remarque :
Attention, il ne faut pas oublier "non croisé" dans l'énoncé de la propriété.
Par exemple AMER est tel que AM=RE et AR=ME,
pourtant AMER n'est pas un parallélogramme car c'est un quadrilatère croisé.
Remarque:
En utilisant la définition du 1) et une propriété du 3 b) du cours on peut déduire la propriété suivante:
Si un quadrilatère non croisé possède deux côtés opposés parallèles et de même longueur
alors ce quadrilatère est un parallélogramme.
Exemple :
DA=ER et (DA)//(ER)
donc DARE est un parallélogramme.
4) Aire du parallélogramme :
L'aire d'un parallélogramme est égale au produit
de la longueur d'un de ses côtés par la hauteur associée.
h est la hauteur associée au côté c et on a : hcAire
×
××
×
=
==
=
h' est la hauteur associée au côté c' et on a :
'
'
hcAire
×
××
×
=
==
=
Rappel :
Pour calculer une aire il faut que toutes les dimensions soient dans la même unité.
c’
h’
h
c
A
E
D
R
Droites parallèles
A M
E R
C H
U
T
On peut calculer de
deux
façons
l’aire du parallélogramme

Vérification de la formule à l’aide d’une figure :
5) Parallélogrammes particuliers :
a) Propriétés communes aux rectangles, losanges et carrés :
 Un rectangle est un parallélogramme particulier.
Démonstration :
ABCD est un rectangle donc il possède 4 angles droits.
(AD) est perpendiculaire à (AB),(BC) est perpendiculaire à (AB),
donc (AD) est parallèle à (BC),
d'après la propriété suivante étudiée en 6
ème
,
si deux droites sont perpendiculaires à une même droite alors ces deux droites sont parallèles.
De même on prouve que (AB) est parallèle à (DC) et donc on peut affirmer que ABCD est un
parallélogramme puisque ses côtés opposés sont parallèles 2 à 2.
 Un losange est un parallélogramme particulier.
Démonstration :
MNOP est un losange
donc il possède 4 cotés de même longueur.
On a en particulier, MN=PO et MP=NO
donc les côtés opposés du losange MNOP ont même longueur,
et ceci prouve que MNOP est un parallélogramme
d'après la propriété suivante,
si un quadrilatère non croisé a ses côtés opposés qui ont la même longueur deux à deux
alors ce quadrilatère est un parallélogramme.
 Un carré est un parallélogramme particulier.
Démonstration :
Un carré est un rectangle particulier (vu en 6
ème
) donc c'est aussi un parallélogramme.
Un rectangle, un losange ou un carré étant des parallélogrammes particuliers, on en déduit que ces
quadrilatères possèdent les mêmes propriétés que le parallélogramme:
 leurs côtés opposés sont parallèles deux à deux,
 leurs côtés opposés sont de même longueur deux à deux,
 leurs diagonales se coupent en leur milieu,
 leur centre de symétrie est le point d’intersection de leurs diagonales.
h
A
c
On « découpe » ce triangle rectangle et on le « place » ici .
Ensuite, on constate que pour calculer l’aire du parallélogramme,
il suffit de calculer l’aire du rectangle ABCD c'est-à-dire c ×
××
× h.
B
C
D
A B
C
D
P
M
N
O