A et B - Mathématiques du Cnam

1
séance n°7
MVA003
Combinatoire, probabilités
ordre, calcul booléen
séance n°7

2
Plan ch8-1
1. Épreuves et événements
2. Fréquences et probabilités
3. Lois de probabilité
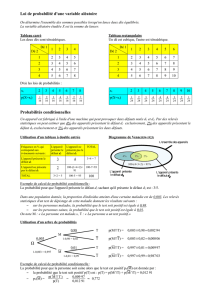
4. Probabilité conditionnelle et indépendance
5. Essais répétés
MVA003
Chapitre 8
Probabilités combinatoires

3
issues
Le calcul des probabilités étudie les phénomènes qui dépendent du
hasard ; on les appelle les phénomènes aléatoires .
Dans un phénomène aléatoire, l'ensemble des résultats théoriquement
possibles s'appelle l' ensemble des épreuves ; on le note .
Un élément de (donc un résultat théoriquement possible) s'appelle une
épreuve ou une issue.
Exemple le lancer de 2 dés, un blanc et un noir.
Exemple le lancer de 2 dés indiscernables.

4
événements
Avec une issue, il arrive qu'un certain événement se produise.
Exemple
Exemple Avec on a sorti un double .
L'ensemble des doubles est :
D = { , , , , , }
Cette liste remplace la définition en compréhension : sortir deux
fois le même numéro , par une définition en extension : on donne
la liste des doubles .
D'une façon générale, on appelle événement toute partie de .
A = { , , , , , , }
Avec cette définition, et sont des événements !
On dit que l'issue x réalise l'événement E quand .
Exemple
langage courant :
langage mathématique :
langage des probabilités : l'issue réalise l'événement D.
est un double.

5
règles de représentation
Règles de représentation
A est un événement
l'issue x réalise l'événement A
langage mathématique langage des probabilités
A est un singleton A est un événement élémentaire
l'événement A entraîne l'événement B
Ac est la non réalisation de A
A et B est la conjonction de A et B
A et B sont incompatibles
A ou B est la disjonction de A et B