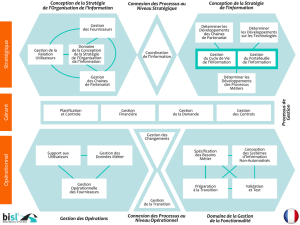
Formules de Taylor, Développements limités - IMJ-PRG

Chapitre 7
Formules de Taylor, Développ ements
limités
7.1 Exercices sur le chapitre 7
Exercice 7.1. Sommes de développements limités.
Déterminer les développements limités suivants :
1) √1−x+√1+xàl’ordre4en0.
2) 1
1−x−e2xàl’ordre3en0.
Exercice 7.2. Produits de développements limités.
Déterminer les développements limités suivants :
1) sin xcos xàl’ordre6en0.
2) (ln (1 + x))2àl’ordre4en0.
Exercice 7.3. Compositions de développements limités.
Déterminer les développements limités suivants :
1) ln !sin x
x"àl’ordre4en0.
2) (cos x)sin xàl’ordre5en0.
Exercice 7.4. Inverses de développements limités.
Déterminer les développements limités suivants :
1) tan xàl’ordre5en0.
2) ln (1 + x)
sin xàl’ordre3en0.

62 Chapitre 7. Formules de Taylor, Développements limités
Exercice 7.5. Développements limités en d’autres points que 0.
Déterminer les développements limités suivants :
1) √xàl’ordre3en1.
2) ln (1 + x2)−2ln xàl’ordre6en+∞.
Exercice 7.6. Calcul de limites de fonctions.
Al’aidededéveloppementslimités,déterminerleslimitessuivantes :
1) lim
x→0
exp(sin x)−exp(tan x)
sin x−tan x.
2) lim
x→0
2x
ln !1+x
1−x".
Exercice 7.7.
Soit fune fonction définie sur R,deuxfoisdérivablesetsoitx∈R.Détermineràl’aide
d’un développement limité la limite suivante :
lim
h→0
f(x−h)−2f(x)+f(x+h)
h2
Exercice 7.8.
1) Donner le développement limité à l’ordre 3en x=0de la fonction √1+x.
2) Même question pour la fonction ln(1 −x).
3) En déduire le développement limité à l’ordre 3en x=0de la fonction
f(x)=x√1+x+ln(1−x)
4) Déterminer la limite de f(x)
x3lorsque x→0.
Exercice 7.9.
1) Former le développement limité à l’ordre 5 au voisinage de 0 des fonctions cos xet
ln (1 + x4).
2) Soit fla fonction dédinie pour x̸=0par
f(x)=
cos −1+x2
2
ln (1 + x4)
Montrer que fadmet une limite lquand x→0et calculer l.
3) On considère la fonction Fdéfinie par
F(x)=f(x)six̸=0 et F(0) = l
Montrer que Fest dérivable en 0 et calculer F′(0).

§7.1. Exercices sur le chapitre 7 63
Exercice 7.10.
Soit fla fonction définie sur Rpar :
f(x)=ex(sin x+cos x)−1
1) Calculer f′(x),f′′(x)et f′′′(x).
2) En utilisant la formule de Taylor-Lagrange, montrer que toutx∈[−π
6,π 6],ona
|f(x)−(2x+x2)|≤|x3|
3) Déterminer le plus grand intervalle Isur lequel fest croissante, déterminer J=f(I)
et montrer que fest une bijection de Isur J.
4) Soit f−1:J→Il’application réciproque de f.Calculer#f−1$′(0).