UE1 seances 4-5 et 6 Géométrie élémentaire

GEOMETRIE ELEMENTAIRE DU PLAN ET DE L'ESPACE
GEOMETRIE PLANE - CONSTRUCTIONS
Exercice 1
1) combien peut-on tracer de droites passant par un point ? et par deux points ?
2) Combien un segment contient-il de points ?
3) Les segments [AB] et [BC] ci-dessous sont-ils égaux ?
Exercice 2
A l’aide du compas, tracer plusieurs points équidistants de deux points donnés A et B. Quelle(s)
constatation(s) pouvez-vous faire ?
Exercice 3
Déduisez de ce qui précède une méthode permettant d’effectuer les tracés suivants à la règle et au
compas :
- Le tracé d’une droite perpendiculaire à une droite donnée D1 ;
- Le tracé de la droite perpendiculaire à une droite donnée D2, cette droite perpendiculaire passant par
un point donné A extérieur à la droite D2. ;
- puis le tracé de la droite parallèle à D2 passant par A.
Exercice 4
Rédiger un programme de construction pour réaliser une figure analogue à la figure ci-dessous :
Exercice 5
Soit l’arc de cercle ci-contre.
Tracez le cercle auquel appartient cet arc de cercle.
Exercice 6
Tracer deux points A et B. En utilisant l’équerre, construire des points M1, M2, M3 et M4 tels que les
droites (A M1) et (B M1), les droites (A M2) et (B M2), les droites (A M3) et (B M3), les droites (A M4)
et (B M4) soient perpendiculaires. Construire d’autres points possédant cette propriété. Que peut-on
dire de ces points ?
Exercice 7
On rappelle que la tangente à un cercle de centre C en un point M situé sur le cercle est la droite
perpendiculaire en M au rayon [CM] de ce cercle.
Tracer un cercle de centre K. Placer sur ce cercle deux points D et F non diamétralement opposés.
Placer le milieu I de [DF]. Tracer les tangentes à ce cercle en D et F, elles se coupent en J. Tracer (KJ).
Que peut-on remarquer ?

Exercice 8
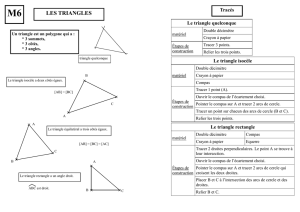
a) Construire, uniquement à la règle et au compas :
- un triangle isocèle ;
- un triangle rectangle ;
- un triangle équilatéral ;
- un triangle connaissant la longueur des trois côtés ;
- un quadrilatère qui a exactement deux angles droits
- un quadrilatère qui a exactement trois angles droits
- un quadrilatère ayant des diagonales perpendiculaires qui ne soit pas un losange
- un quadrilatère ayant des diagonales de même longueur et qui ne soit pas un rectangle
- un rectangle dont la diagonale a une longueur double de celle de l’un des côtés.
b) Tracer un cercle de centre O. Soit P un point de ce cercle. Construire un carré de centre O et dont P
est un sommet.
Exercice 9
Placer trois points I, J, et K non alignés. Pour construire le point L tel que IJKL soit un
parallélogramme, trouver trois méthodes de construction en précisant chaque fois, la propriété
utilisée.
En déduire une autre construction possible d’une droite parallèle à une droite donnée (d)
passant par un point n’appartenant pas à (d)
Exercice 10 : construction de quadrilatères
1. Construire un carré dont la diagonale a pour longueur 4 cm
2. Tracer un point I .Dessiner un carré de centre I et dont le côté a pour longueur 6cm
3. Placer deux points A et I distants de 4 cm .Construire un losange dont un
sommet est A et dont le centre est I
4. Placer deux points A et I distants de 3 cm. Construire un parallélogramme dont un
sommet est A et I le centre avec des côtés de longueurs respectives 3cm et 5 cm
Exercice 11
Tracer en utilisant uniquement la règle et le compas :
a) un angle de 90° ; b) un angle de 45° ; un angle de 60) ; un angle de 30°
Exercice 12
a) Partager l’angle ci-dessous en deux parties égales. Quel est le nom de la droite que vous avez
tracée ?
b) écrire un programme de construction qui permette de construire cette droite avec la règle et
le compas.
Exercice 13
Tracer un triangle ABC ainsi que les trois bissectrices des trois angles de ce triangle. Que peut-
on remarquer ? Tracer la perpendiculaire à l’un des côtés du triangle qui passe par le point
d’intersection K des deux bissectrices. Elle coupe ce côté en un point H. Tracer le cercle de
centre K et de rayon [HK]. Que peut-on remarquer ?

Exercice 14
a) Soit A et B deux points distincts. Combien peut-on tracer de cercles passant par ces
deux points ? Quel est l’ensemble des centres de ces cercles ?
b) Combien peut-on tracer de cercles passant par trois points distincts A, B et C ? tracer la
figure correspondante.
Exercice 15
a) définir la droite que l’on appelle hauteur d’un triangle et la droite que l’on appelle
médiane d’un triangle
b) Combien de hauteurs et de médianes peut-on tracer pour un triangle quelconque ABC ?
tracer ces droites (une hauteur sera tracée en bleue et une médiane en rouge). Que
remarquez-vous ?
c) Tracer un triangle et placer l’orthocentre, le centre de gravité et le centre du cercle
circonscrit. Que remarquez-vous ?
Exercice 16 :
1. Construire le sommet C du triangle ABC sachant que la droite (d) est à la fois bissectrice de
l'angle BAC et la hauteur issue de A
A
2. Construire le sommet C du triangle ABC sachant que la droite (d1) est la hauteur issue de A et
la droite (d2) est la médiane issue de A.

Exercice 17
Tracer sur la copie une figure ressemblant à celle ci-dessous : Il ne s’agit pas de reproduire exactement
cette figure mais d’en respecter la forme et la disposition.
Puis :
Construire à la règle et au compas les symétriques A', B' et C' des points A, B et C par rapport à
la droite (OI) en laissant apparents les traits de construction.
Construire à la règle et au compas les symétriques A", B" et C" des points A', B' et C' par rapport
à la droite (OJ) en laissant apparents les traits de construction.

CUBE ET PRISME
Exercice 1
Compléter le cube en perspective cavalière. Mettre en pointillé les traits cachés.
Compléter le prisme en perspective cavalière. Mettre en pointillé les traits cachés.