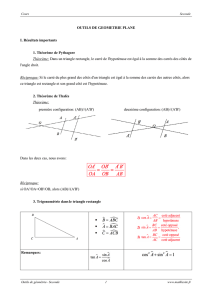
Corrigé 2

Thème : Géométrie plane
I- Situation du thème dans le programme :
Primaire : Géométrie perceptive et instrumentée.
6e : Apparition de la géométrie déductive avec :
- rectangle, carré, losange, cercle, triangles usuels.
-médiatrice et bissectrice.
-Symétrie axiale.
5e : Activités pour expérimenter et conjecturer.
-Symétrie centrale.
-parallélogramme. Trop détaillé
-droites remarquables dans un triangle.
4e : Triangles : -Milieux et parallèles.
-Rectangle.
Agrandissement et réduction.
3e : Thalès.
Angles inscrits, angles au centre.
2nd : La géométrie devient repérée :
-Coordonnées d’un point du plan.
-Droites : fonction affine.
-Vecteurs.
1re : Vecteurs : Colinéarité, équation cartésienne.
Produit scalaire dans le plan.
Tle : Nombres complexes.
La géométrie tient une grande place dans les programmes de la Primaire jusqu’à la Terminale. Dès
l’école élémentaire, la géométrie est introduite par la reconnaissance perceptive (reconnaissance des
formes) puis, laisse place à une géométrie plus analytique qui s’appuie sur une vérification à l’aide
d’instruments. C’est à partir de la sixième que l’on voit apparaître la géométrie déductive qui
consiste à structurer et hiérarchiser des connaissances. En cinquième on commence à faire des
activités afin d’expérimenter et conjecturer. On y étudie alors la symétrie centrale et les propriétés
du parallélogramme, qui sont suivis en quatrième par l’étude du théorème des milieux dans un
triangle et d’une première configuration du théorème de Thalès. La deuxième configuration est vue
en classe de troisième.
On voit ensuite l’apparition d’une géométrie repérée à partir de la seconde qui permet de résoudre
des problèmes.
II- Situation de l’exercice dans le thème :
Peut être proposé à deux niveaux : - En cinquième en utilisant les propriétés du parallélogramme ou
la symétrie.
- En quatrième en utilisant le théorème des milieux et sa
réciproque.
Mais plutôt réservé à une classe de quatrième.
Ici, on peut le situer en classe de quatrième en tant que : - soit introduction au théorème des milieux.
- soit en application de ce même théorème.

III- Travail à exposer devant le jury :
1) De quels acquis témoignent les productions des trois élèves dans le domaine de la géométrie
plane ?
L’élève 1 :
 Les points positifs : - Si I milieu de [AB] ⇔ AI=IB
- Technique expérimentale : construction à la règle graduée.
- Mesure de longueurs.
 Ce qui est moins bien : - Unique instrument utilisé : la règle graduée.
- Construction non précise (« approchée »).
- Non pas « glisser » mais « pivoter ».
- Reste sur ses acquis de 6e (mesure de longueurs et équidistance
(médiatrice)).
Ne pratique pas de la géométrie déductive mais plutôt empirique, instrumentée.
L’élève 2 :
 Les points positifs : - Idée de prendre le problème « à l’envers » partir des points déjà placés.
- Notion d’agrandissement et de réduction (au programme de 4e) donc on
peut supposer qu’il sait que cela conserve les milieux, les parallèles et
les angles, afin que sa reproduction puisse se superposer.
- Expérimentation graphique et raisonnement d’analyse-synthèse sans
réellement de synthèse car il énonce seulement ce qu’il faut faire « il
ne reste plus qu’à agrandir… ».
Il a tracé 2 droites que l’on suppose former le même angle que l’énoncé. Il a placé A et B ainsi que le
point I milieu de [AB]. Il obtient donc une figure qui vérifie l’énoncé et déduit que s’il place le milieu J
de [OA], la droite (JI) est parallèle à D’. C’est une bonne démarche d’analyse de la figure mais la
dernière phrase montre qu’il n’a pas réalisé « l’agrandissement », donc s’il a fait un calque de la
figure de l’énoncé, les points I ne coïncideront pas.
 Ce qui est moins bien : - Manque d’explications car on ne sait pas comment il à réussit à
obtenir que (IJ) est parallèle à D’, les points A et B semblant être placés arbitrairement.
- N’exploite pas son idée jusqu’au bout, c’est-à-dire que à partir de sa
construction il pourrait trouver le facteur k d’agrandissement grâce au
rapport de la longueur OI sur son dessin et sur celui de l’énoncé.
- N’exploite pas sa remarque sur les droites parallèles. Il aurait ainsi
pût trouver, à partir de son expérimentation, une autre manière
d’aboutir au résultat par le théorème des milieux.
On est pas certain d’avoir compris ce qu’il a fait. Il observe quelque chose mais pourquoi croit-il que
en agrandissant il arrivera au résultat ?
L’élève 3 :
 Les points positifs : - Résolution du problème grâce à une notion déjà connue : la symétrie.
Il montre qu’il connaît le contrat implicite entre le professeur et les élèves en disant « on est dans le
chapitre…», il fait donc la relation avec ce que le professeur fait en cours et ce qu’il donne comme
exercice.
 Ce qui est moins bien : - Ne précise pas la symétrie utilisée, mais d’après le dessin on suppose
qu’il s’agit de la symétrie centrale.
- Ne justifie pas son résultat, on suppose que « Ca marche ! » signifie
qu’il a mesuré les longueurs AI et IB sur sa construction.
- Ne justifie pas pourquoi les points A et B sont aux intersections des
droites.

2) Exposer une correction de l’exercice telle que vous la présenteriez devant une classe de
quatrième, prenant en compte les productions des élèves.
Une correction de cet exercice s’effectue en classe de quatrième grâce à la réciproque du théorème
des milieux : dans un triangle, si une droite passe par le milieu d’un côté et est parallèle à un
deuxième côté, alors elle passe par le milieu du troisième côté.
On voit que l’élève 2 est le plus proche de cette résolution car il utilise des éléments de ce
théorème : il place le point J milieu de [OA] et remarque que (IJ) est parallèle à D’. Mais il
n’approfondit pas dans ce sens.
Ainsi je vais vous présenter une correction de cet exercice :
1) On nomme O le point d’intersection de D et D’.
2) Tracer la parallèle, passant par I, à la droite D’, par exemple.
3) On nomme J le point d’intersection de cette parallèle avec la droite D.
4) Placer le point A sur D.
5) Tracer la droite (AI).
6) Le point B est le point d’intersection entre (AI) et D’.
(EXERCICE DETAILLE EN ANNEXE)
3) Proposer deux ou trois exercices sur le thème géométrie plane, dont l’un au moins peut conduire à
l’utilisation d’un logiciel de géométrie.
Exercice 1 : Le sommet C du parallélogramme ABCD est sorti des limites de la feuille. Tracer
la partie visible de la droite (AC) sans construire le point C.
D
A B
Le jury n’interrogerait pas sur cet exercice car il est simple.
Pourquoi ce choix : - Exercice de cinquième.
- Original.
- Permet de vérifier la maîtrise des propriétés sur le parallélogramme
essentiellement la propriété sur les diagonale qui se coupent en leur milieu.
- Demande de savoir les outils qu’il faut pour tracer une droite, à savoir : deux
points.

Exercice 2 : Sur le schéma, les points B et C
matérialisent deux pieds de la tour Eiffel et le point
A est un point du deuxième étage. Le segment [IJ]
symbolise le premier étage. Calculer la longueur IJ.
Justifier la réponse.
Pourquoi ce choix : - Exercice de quatrième.
- Application du théorème des
milieux.
- Demande un peut de recherche
pour un élève de quatrième
avant d’aboutir à l’utilisation du
théorème car on ne donne
aucune indication sur
l’emplacement des points si ce
n’est des longueurs.
Trop d’exercices ciblé sur la géométrie des collèges, c’est mieux de prendre des exercices de
plusieurs niveaux comme un de troisième et un de terminale, par exemple sur les complexes.
Exercice 3 : ABC est un triangle rectangle en A tel que : AB= 4 cm et AC= 3 cm.
M est un point du segment [AB].
La parallèle à (AC) passant par M coupe (BC) en N.
La parallèle à (BC) passant par M coupe (AC) en P.
On se propose d’établir une relation entre la longueur AM et
le périmètre, en cm, du parallélogramme CNMP.
1) Conjecturer :
a) Avec un logiciel de géométrie, faire cette figure ;
afficher la longueur AM et le périmètre p de CNMP.
b) Déplacer le point M sur [AB], c’est-à-dire
prendre plusieurs valeurs de AM en commençant par AM=0.
Conjecturer une expression de p en fonction de AM.
2) Démontrer :
a) Calculer BC.
b) On pose AM= x cm. A l’aide du théorème de Thalès, exprimer les longueurs PM et AP en
fonction de x.
c) En déduire l’expression de p en fonction de x.
Pourquoi ce choix : - Exercice de troisième.
- Application du théorème de Thalès.
- Demande une recherche de la part des élèves pour la conjecture et pour trouver
l’expression du périmètre.
- Suite du programme de quatrième sur les théorèmes des milieux et des trois
rapports égaux.

IV- Annexes :
Résolution de l’exercice comme il faudrait le faire en classe de quatrième :
On écrit la réciproque du théorème des milieux au tableau.
« Dans un triangle, si une droite passe par le milieu d’un côté et est parallèle à un deuxième côté,
alors elle passe par le milieu du troisième côté. »
1) Je nomme O le point d’intersection des deux droites D et D’. On nous demande de trouver deux
points A et B tels que A soit sur D et B soit sur D’. On aura donc trois points qui formeront un triangle,
et ainsi la première hypothèse de la réciproque, qui est de ce placer dans un triangle, est vérifiée.
2) Les deux autres hypothèses sont : - une droite passant par le milieu d’un côté
- cette même droite est parallèle à un second côté.
D’après l’énoncé on a I milieu de [AB], donc on a bien un milieu d’un des côtés du triangle ABC. On
peut ainsi tracer une droite parallèle à un second côté passant par I. Cette droite sera parallèle à D ou
à D’. Je choisis qu’elle soit parallèle à D’.
A l’aide de ma règle et de mon compas je trace cette droite parallèle à D’ et passant par I :
D
O I
D’
(Je mets la pointe de mon compas sur un point de D’ et je prends l’écartement entre ce point et I. Je
mets la pointe du compas sur O en gardant l’écartement, et je trace un arc de cercle. Je prends
l’écartement entre le point et O, et je le reporte sur I)
3) La conclusion de la réciproque est que cette droite tracée passe par le milieu du troisième côté du
triangle. Donc le point d’intersection entre la droite parallèle passant par I et D est le milieu du côté
OA du triangle. On le nomme J par exemple.
4) Maintenant comme on sait que J est le milieu de [OA], alors on a OJ=JA. Ainsi pour placer le point
A, on prend la mesure de OJ avec le compas et on la reporte en plaçant la point du compas sur J. on
obtient le point A :
A D
J
O I
D’
5) Il ne reste plus qu’à tracer la droite (AI) et le point d’intersection de (AI) et D’ est le point B :
A
D
O J I
B D
On peut vérifier avec le compas que l’on a bien AI=IB.