07 Angles.6èA - Collège Le Grand Clos

CH VIII ANGLES
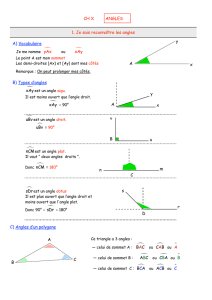
1. Je sais reconnaître les angles
A) Vocabulaire
Je me nomme
yAx
∑
ou
xAy
∑
Le point A est mon sommet
Les demi-droites [Ax) et [Ay) sont mes côtés
Remarque : On peut prolonger mes côtés.
B) Types d’angles
xAy
∑
est un angle aigu.
Il est moins ouvert que l’angle droit.
xAy
∑
≺ 90°
uBv
∑
est un angle droit.
uBv
∑
= 90°
nCM
∑
est un angle plat.
Il vaut “ deux angles droits ”.
Donc
nCM
∑
= 180°
sDr
∑
est un angle obtus.
Il est plus ouvert que l’angle droit et
moins ouvert que l'angle plat.
Donc 90° ≺
sDr
∑
≺ 180°
C) Angles d’un polygone
Ce triangle a 3 angles :
— celui de sommet A :
BAC
∑
ou
CAB
∑
ou
A
µ
— celui de sommet B :
ABC
∑
ou
CBA
∑
ou
B
$
— celui de sommet C :
BCA
∑
ou
ACB
∑
ou
C
$
x
A
y
A
C
B
Ax
y
C
m
n
D
r
s
Bu
v

2. Je sais utiliser le rapporteur.
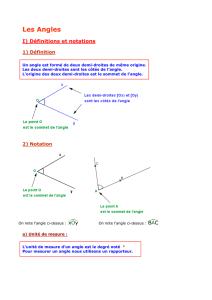
A) L’unité d’angle
L’unité d’angle est le degré. Le symbole du degré est °
Voici un angle de 1° et un angle de 5°.
B) L’angle droit
BAC
∑
= 90°
C) Mesurer un angle : On utilise un rapporteur
AOB
∑
= 120°
Exemples :
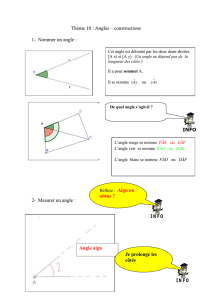
D) Tracer un angle de mesure donnée
Construire un angle de 25° et un angle de 138°
AC
B
1°) On fait coïncider le centre du rapporteur
avec le sommet O de l’angle
2°) On positionne le 0°
sur le côté [OA) de l’angle
3°) On lit la mesure de l’angle sur le côté [OB)
27°
130°
28°
110°
42°

x'
A'
1°) Je trace un premier côté de l’angle : [A'x').
Ax
y
2°) Je trace deux arcs de même rayon l’un de centre A et l’autre de centre A'.
y
x
A
T
R
x'
A'
M
3°) Je prends l’écartement entre R et T et je le reporte à partir du point M.
Il coupe le premier arc en N. Je trace le deuxième côté de l’angle : [A'N)
R
T
A
y
xx'
A'
N
M
3. Angles égaux. Reproduire un angle au compas.
A) Codage
Le triangle EFG est isocèle en E.
G
µ
= 70°
F
$
= 70°
On code qu’ils sont égaux..
B) Reproduire un angle
On peut utiliser le compas.
E
F
G

4. La bissectrice d’un angle. Je sais calculer un angle.
A) Définition
La bissectrice d’un angle est la demi-droite qui partage cet angle en deux angles égaux.
B) Tracer la bissectrice
Avec le rapporteur
C) Calculer un angle
1°) Calculer l' angle
DAE
∑
2°) Construire les bissectrices
[Ay) de l’angle
DAE
∑
et [Ax) de l’angle
3°) Démontrer que [Ax) ⊥ [Ay)
Solution
1°)
DAE
∑
= 180° - 62°
DAE
∑
= 118°
2°) On trace les bissectrices
3°) On calcule l'angle
xAy
∑
xAy
∑
= ( 62° : 2 ) + ( 118° : 2 )
xAy
∑
= 31° + 59°
xAy
∑
= 90°
Conclusion : [Ax) ⊥ [Ay)
34° : 2 = 17°
AC
B
17°
17°
A
E
B
D
62°
BAD
A
E
B
D
x
y
118°
62°