mecanique_2eme periode2009

- 1 -
PCSI-MPSI
2ème Période
Modélisation cinématique
des mécanismes
Statique du solide
D.Feautrier

- 2 - Méthode d’analyse d’un mécanisme
Partie 1
Méthode d’analyse d’un mécanisme
1.1 Modélisation des liaisons
1.1.1 Introduction
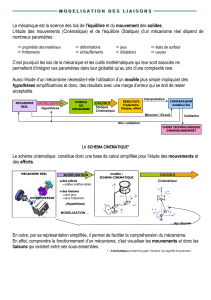
L’objectif de ce chapitre est de donner une méthode qui permet de construire un schéma cinématique d’un
mécanisme. Pour cela il faut être capable de modéliser cinématiquement les liaisons entre les différents
solides composant un mécanisme donné.
1.1.2 Classe d’équivalence cinématique
L’ensemble des solides d’un mécanisme sans mouvement relatif constitue une classe d’équivalence ciné-
matique.
En général, pour plus de clarté, on numérote les classes d’équivalence.

- 3 -
1.1.3 Analyse des zones de contact entre classes d’équivalence
1.2 Cinématique du contact ponctuel
Soient deux solides et en contact ponctuel au point . Soit le plan tangent à et en .
Afin de déterminer le modèle cinématique associé à une liaison mécanique, il convient d’analyser la
géométrie des zones de contact entre les deux classes d’équivalence.
On distingue trois types de géométrie des zones de contact :
• Contact ponctuel
• Contact linéaire
• Contact surfacique
Le tableau suivant regroupe les différentes possibilités d'associations de surfaces élémentaires :
12 IΠ12 P

- 4 - Méthode d’analyse d’un mécanisme
Le torseur cinématique de par rapport à s’écrit en P :
Par définition, on appelle vecteur vitesse de glissement au point le vecteur
On pose où :
• est appelé vecteur rotation de pivotement
• est appelé vecteur rotation de roulement
Propriété : Le vecteur vitesse de glissement du point du solide par rapport au solide appartient au
plan tangent .
Remarque : On dit qu’il y a roulement sans glissement si
, et
1.3 Liaisons normalisées
1.3.1 Repère local associé à une liaison
Les liaisons les plus courantes rencontrées en mécaniques sont normalisées. Cette norme à uniquement
pour but de définir des possibilités de mouvement autorisées par une liaisons entre deux classes d’équiva-
lence sans préjuger de la conception technologique de la liaison.
Les mouvements relatifs autorisé dépendent de la nature des surfaces en contact. Les surfaces prises en
comte par la désignation normalisée sont les surfaces simples : sphère, plan, cylindre. L’association des
surfaces donnent des contacts ponctuels, linéiques ou surfaciques de formes diverses. C’est de l’associa-
tions de ces surfaces que résultent les mouvements possibles.
21 V21⁄(){}
Ω21⁄()
VP 21⁄∈()
P
=
PVPS
2S1
⁄∈()
Ω21⁄()Ω
n21⁄()Ω t21⁄()+=
Ωn21⁄()
Ωt21⁄()
P21
Π
VP2 1⁄,()0= Ωn21⁄()0= Ωt21⁄()0≠()

- 5 -
Pour décrire à un instant donné les translations
et les rotations autorisées par une liaison, on
place judicieusement sur cette liaison un repère
de façon à décomposer le mou-
vement relatif entre les deux solides en six
mouvements élémentaires qui seront paramé-
trés par six paramètres (position et orientation)
indépendants : trois translations d’axe , ou
et trois rotations autour des axes ,
et . Le repère est
appelé repère local associé à une liaisons.
1.3.2 Degrés de liberté d’une liaison
Le nombre de degrés de liberté d’une liaison entre deux solides est le nombre de mouvements élémentaires
indépendants que la liaison autorise (nombre de rotations et de translations suivant les axes du repère
local). Il est au maximum de six (voir chapitre «paramétrés de la position de deux solides dans l’espace»).
1.3.3 Modèles cinématiques associés aux liaisons
En fonction de la géométrie de la zone de contact on va autoriser ou supprimer des degrés de liberté.
ROxyz,,,()
x
y
zOx,()
Oy,()Oz,() ROxyz,,,()
*