chapitre 8 : les parallelogrammes

CHAPITRE 8 : LES PARALLELOGRAMMES
1) Le parallélogramme :
a) Introduction et définition :
Voici un quadrilatère quelconque.
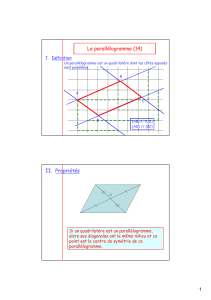
Parmi les quadrilatères, ceux qui ont 2 côtés opposés parallèles s’appellent les trapèzes.
Parmi les trapèzes, ceux qui ont les côtés opposés parallèles s’appellent les parallélogrammes.
Définition :
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
Exemple :
ABCD est un parallélogramme :
(AB) // (CD) et (AD) // (BC)
Fiche 1 : les parallélogrammes (vocabulaire, nommer un parallélogramme)
Fiche 2 : les parallélogrammes (définition)
Fiche d’activité 1 : centre de symétrie d’un parallélogramme
b) Propriétés du parallélogramme :
Propriété :
Un parallélogramme admet un centre de symétrie qui est le point d’intersection des diagonales.
On a alors comme conséquence les propriétés suivantes :
Propriétés :
1) Les diagonales d’un parallélogramme se coupent en leur milieu.
2) Les côtés opposés d’un parallélogramme ont la même longueur.
3) Les angles opposés d’un parallélogramme ont la même mesure.
2 Côtés
opposés
parallèles
2 Côtés
opposés
parallèles
A B
C D
Côtés opposés : [AB] et [DC] Côtés consécutifs : [DC] et [BC]

Exemple :
1) Les diagonales se coupent en leur milieu :
I est le milieu de [AC] et le milieu de [BD]
2) Les côtés opposés ont la même longueur :
AB = DC et AD = BC
3) Les angles opposés ont la même mesure :
A = C et B = D
Méthode de construction :
On veut terminer le parallélogramme ABCD à partir des points A, B et C.
Fiche 3 : construction de parallélogrammes
Fiche 4 : construction de parallélogrammes
Fiche 5 : construction de parallélogrammes
Fiche 6 : construction de parallélogrammes
Fiche 7 : parallélogramme et diagonales
2) Reconnaître un parallélogramme:
Propriété 1:
Un quadrilatère dont les diagonales se coupent en leur milieu est un parallélogramme.
Exemple :
Puisque les diagonales [PA] et [LT] du quadrilatère PLAT
se coupent en leur milieu alors PLAT est un parallélogramme.
Fiche 8 : Montrer qu’un quadrilatère est un parallélogramme
B
C
A
1.
On trace [AB] et [BC] puis on prend la distance entre A
et B… … et on la reporte à partir de C
B
C
A
B
C
A
2. On prend la distance entre B et C… … et on la reporte à partir de A. Le point d’intersection
des deux arcs est D.
B
C
A
D
P
L
A
T

Propriété 2:
Un quadrilatère non croisé dont les côtés opposés ont la même longueur est un parallélogramme.
Exemple :
ABCD un quadrilatère non croisé. Puisque AB = CD et AD = BC
alors ABCD est un parallélogramme.
Propriété 3:
Un quadrilatère non croisé dont 2 côtés opposés sont parallèles et de même longueur est un
parallélogramme.
Exemple :
ABCD un quadrilatère non croisé. Puisque (AB) // (CD) et
AB = CD alors ABCD est un parallélogramme.
Exercices n°18, 21, 22 page 215
A
B
C
D
A
B
C
D