ELCINQ_02 Resistances associations et diviseurs

G.P. Questions de cours électrocinétique
Association de résistances :
Démontrer la formule d'association des résistances en série, des résistances en parallèle
Démontrer la formule des diviseurs de tension, des diviseurs de courant. Préciser les
conditions d'utilisation de ces formules.
En utilisant ces méthodes, résoudre les deux exercices proposés. Proposer une autre méthode
de résolution.
Réponse:
Lois d'association des résistances:
en série:
u=u1u2u3
E0
R1R2
R4
R3
V ?
R1
R2
R4
R3
I0I ?
R3R2R1
i
u3u2u1
u

G.P. Questions de cours électrocinétique
u=R1iR2iR3i
u=R1R2R3i
L'ensemble se comporte donc comme une résistance égale à la somme des résistances.
Req=R1R2R3
en parallèle:
i=i1i2i3
i=G1uG2uG3u
i=G1G2G3u
L'ensemble se comporte donc comme une conductance égale à la somme des conductances.
Geq=G1G2G3
Formule des diviseurs:
de tension:
u=R1R2R3i
u1=R1i
donc
R1
R2
R3
i
u
i1
i2
i3
u1
R3R2R1
i
u
i ' = 0

G.P. Questions de cours électrocinétique
u1
u=R1 R1R2R3
il faut que la sortie du diviseur soit à vide pour que toute l'intensité parcourt la résistance
considérée.
de courant:
i=G1G2G3u
i1=G1u
donc
i1
i=G1 G1G2G3
il faut que la sortie du diviseur soit en court-circuit pour que toute la tension soit aux bornes de la
conductance considérée.
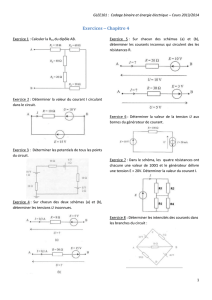
Exercice 1:
L'intensité, délivrée par le générateur, parcourt la résistance
R1R2// R3R4= R11
G2G34 
avec
G34=1/ R3R4
(association de résistances). La
tension aux bornes de
R2// R3R4
vaut donc
E0
1
G2G34 
1
G1
1
G2G34 
=E0
G1
G2G34 G1
(diviseur de tension). On a donc obtenu la tension aux bornes de
R3R4
et finalement
V=E0
G1
G2G34G1
R4
R3R4=E0
G1
G2G34 G1
G3
G4G3
(diviseur de tension).
V=E0
G1G3
G1G3G1G4G2G3G2G4G3G4
ou
R1
R2
R3
i
u
i1
u' = 0

G.P. Questions de cours électrocinétique
V=E0
R2R4
R1R2R1R3R1R4R2R3R2R4
Autre méthode:
Le générateur de Thévenin est transformé en générateur de Norton (courant
G1E0
, conductance
interne
G1
). Ce générateur de courant
G1E0
débite dans trois conductances en parallèle
G1
,
G2
,
G34=1/ R3R4
. La formule des diviseurs de courant donne l'intensité dans
G34
:
G34
G1G2G34G1 E0
et la loi d'Ohm donne la tension cherchée en multipliant par
R4
c'est à
dire en divisant par
G4
:
V=G1G34
G4G1G2G34E0
(vérifier que cela donne le même résultat).
Exercice 2:
La tension du générateur est appliquée à la conductance
G11
R2R34 
avec
R34=1
G3G4
(association de résistances). L'intensité dans
R2R3// R4
de vaut donc
I0
1
R2R34 
1
R1
1
R2R34 
=I0
R1
R2R34 R1
(diviseur de courant). On a donc obtenu l'intensité totale
dans
R3// R4
et finalement
I=I0
R1
R2R34 R1
G4
G3G4
(diviseur de courant).
I=I0
R1R3
R1R3R1R4R2R3R2R4R3R4
ou
I=I0
G2G4
G1G2G1G3G1G4G2G3G2G4
Autre méthode:
Le générateur de Norton est transformé en générateur de Thévenin (force électromotrice
R1I0
,
résistance interne
R1
). Ce générateur de force électromotrice
R1I0
débite dans trois résistances
en série
R1
,
R2
,
R34=1/G3G4
. La formule des diviseurs de tension donne la tension aux
bornes de
R34
:
R34
R1R2R34 R1I0
et la loi d'Ohm donne la tension cherchée en multipliant par
G4
c'est à dire en divisant par
R4
:
I=R1R34
R4R1R2R34 I0
(vérifier que cela donne le même
résultat).