Corrigé DS6 - Dominique Frin

CORRIGÉ DEVOIR SURVEILLÉ N° 6 TERMINALE ES spé
Deux fabricants de parfum lancent simultanément leur nouveau produit qu’ils nomment respectivement Aurore et
Boréale. Afin de promouvoir celui-ci, chacun organise une campagne de publicité.
L’un d’eux contrôle l’efficacité de sa campagne par des sondages hebdomadaires.
Chaque semaine, il interroge les mêmes personnes qui toutes se prononcent en faveur de l’un de ces deux produits.
Au début de la campagne, 20 % des personnes interrogées préfèrent Aurore et les autres préfèrent Boréale.
Les arguments publicitaires font évoluer cette répartition :
10 % des personnes préférant Aurore et 15 % des personnes préférant Boréale changent d’avis d’une semaine sur
l’autre. La semaine du début de la campagne est notée semaine 0.
Pour tout entier naturel n, l’état probabiliste de la semaine n est défini par la matrice ligne Pn = (an bn ), où an
désigne la probabilité qu’une personne interrogée au hasard préfère Aurore la semaine n et bn la probabilité que
cette personne préfère Boréale la semaine n.
1. La matrice ligne P0 de l’état probabiliste initial et donc P0 = (0,2 0,8).
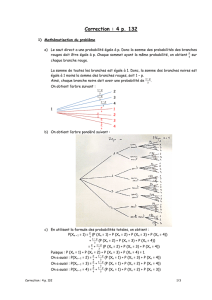
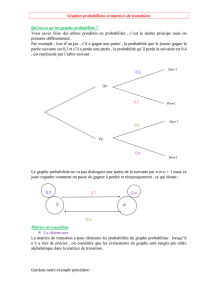
2. Le graphe probabiliste de sommets A et B, A pour Aurore et B
pour Boréale représentant la situation :
3. a) La matrice de transition M de ce graphe en respectant l’ordre
alphabétique des sommets : M =
(
0,9 0,1
0,15 0,85
)
.
b) La matrice ligne P1 = P0 M = (0,3 0,7) donnant l’état probabiliste la semaine 1.
4. La matrice ligne P10 = P0 M10 = (0,577 0,423). La dixième semaine, environ 57,7 % des personnes interrogées
préfèrent Aurore et 42,3 % préfèrent Boréale.
5. Pour tout entier naturel n, on a an + bn = 1, donc bn = 1 – an .
Pn + 1 = (an + 1 bn + 1) = Pn M = (an bn)
(
0,9 0,1
0,15 0,85
)
= (0,9an + 0,15bn 0,1an + 0,85bn ) ,
donc an + 1 = 0,9an + 0,15bn = 0,9an + 0,15(1 – an) = 0,75an + 0,15.
6. On considère la suite (un) définie pour tout entier n par un = an – 0,6.
a) Pour tout entier naturel n, un + 1 = an + 1 – 0,6 = 0,75an + 0,15 – 0,6 = 0,75an – 0,45 = 0,75(an – 0,6) = 0,75un .
Donc la suite (un) est une suite géométrique de raison 0,75 et de premier terme u0 = a0 – 0,6 = 0,2 – 0,6 = – 0,4.
b) Ainsi, un = – 0,4×(0,75)n . La raison de la suite est strictement comprise entre 0 et 1, donc la suite converge vers
0, soit
lim
n→+∞
un
= 0.
c) Comme un = an – 0,6, on en déduit que an = un + 0,6 = – 0,4×(0,75)n + 0,6 et que
lim
n→+∞
an
= 0,6.
7. L'état stable du graphe probabiliste est (0,6 0,4) puisque cet état stable (a b) vérifie a =
lim
n→+∞
an
et b = 1 – a.
BONUS : Soit P = (a b) la matrice ligne de l’état probabiliste stable.
On a alors P = PM, soit (a b) = (a b)
(
0,9 0,1
0,15 0,85
)
= (0,9a + 0,15b 0,1a + 0,85b), d'où le système :
{
a=0,9a+0,15 b
b=0,1a+0,85 b
a+b=1
équivaut à
{
0,1a−0,15 b=0
−0,1a+0,15 b=0
a+b=1
équivaut à
(
0,1 −0,15
1 1
)
(
a
b
)
=
(
0
1
)
.
On pose A =
(
0,1 −0,15
1 1
)
, X =
(
a
b
)
et B =
(
0
1
)
; le système équivaut à AX = B qui équivaut à
X = A– 1B =
(
0,6
0,4
)
, donc a = 0,6, b = 0,4.