Tableau d`effectifs et calculs

Statistiques en psychologie.
Étude d'une variable.
2 variables possibles :
► variable qualitative :
Situation
Exemple
Org° des données
Représ° graphique
Détermination possible
Variable qualitative
nominale
Zone d'habitation
Tableau d'effectifs
Diagramme en barre,
Diagramme en secteur,
Diagramme unicolonne
Mode
Variable qualitative
ordinale
Niveau d’adéquation
( de 1 à 5)
Puissance
(de Faible à Fort )
Tableau d'effectifs
Diagramme en barre,
Diagramme en secteur,
Diagramme unicolonne
Mode,
Médiane,
Quartile
► variable quantitative :
Situation
Exemple
Org° des données
Représ° graphique
Détermination possible
1 -Variable quantitative
discrète
Nombre précis de
personne
( {1,2,3...} )
AGE
Tableau d'effectifs
Diagramme en baton
Mode,
Médiane,
Quartiles,
Moyenne,
Variance,
Écart-type
2 -Variable quantitative
continue
Temps, durée
( toutes les valeurs
positives ( ]0, +inf[ )
Tableau d'effectifs
(modalité = classes)
Histogramme
Idem
Mode : Valeur la plus élevé ( modalité avec l'effectif le plus grand ), sur un graphique c'est le pic le plus haut.
Médiane : Modalité séparant l'échantillon N en deux parties de même taille.
Calcul : 1. On calcule N/2
2. On sélectionne l'effectif cumulé N. Immédiatement supérieur à N/2
Quartiles : Modalités notées Q1, Q2, et Q3 séparant l'échantillon en quatre partie de taille semblable.
Calcul : Q1 = N/4 Q2 = médiane = N/2 Q3 = (3xN) /4
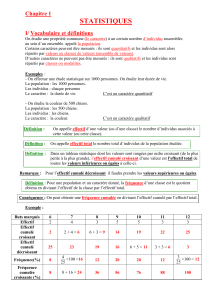
Tableau d'effectifs et calculs :
Modalité
Effectifs
Fréquences
Pourcentage
Effectifs
cumulés
Ni x Xi
Ni x (Xi)²
Moyenne
Variance
Écart type
Notation
( x1, x2, x3.. )
( n1, n2, n3.. )
( f1, f2, f3.. )
( N1, N2,
N3.. )
X
Var (X)
Ox
Calcul
- f1 = n1/N
- f2 = n2/N
- f3 =
n3/N...
- f1 x 100
- f2 x 100
- f3 x 100..
- N1 = n1
- N2 = n1+n2
- N3= N2+n3..
- n1 x x1
- n2 x x2
- n3 x x3..
- n1 x (x1)²
- n2 x (x2)²
- n3 x (x3)² ..
S1/N
S2/N -
(
var(x)
Total
N
1
100
S1
S2
Étude d'un couple de variable.

Situation
Exemple
Org° des données
Représent° graphique
Détermination
possible
Couple de variables
(X,Y)
X = Statut
(locataire/propriétaire)
Y = Lieu
(zone d'habitat)
Tableau des
effectifs conjoints
Distribution conjointe,
Distribution marginale,
Distribution conditionnelle
Khi – deux
V de Cramér
Coef phi
Explication par exercice (chapitre 3- exercice 15)
● Étape 1 : Faire un tableau de distribution conjointe.
Donner la distribution marginale
▼X Y►
Père né en
France
Père né à
l'étranger
Effectif de X n i,.
Mère née en France
129
(n 1,1)
17
(n 1/2)
146
Mère née à l'étranger
13
(n 2,1)
30
(n 2,2)
43
Effectif de X n .,i
142
47
N = 189
● Étape 2 : Faire un tableau de distribution conditionnelle.
► 2 possibilités : - distribution de X conditionnellement à Y
- distribution de Y conditionnellement à X
Distribution de X conditionnellement à Y :
▼X Y►
Père né en France
Père né à l'étranger
Mère née en France
129/142 = 91%
17/47 = 36%
Mère née à l'étranger
13/142 = 9%
30/47 = 64%
Distribution de Y conditionnellement à X :
▼X Y►
Père né en France
Père né à l'étranger
Mère née en France
129/146 = 88%
17/146 = 12%
Mère née à l'étranger
13/43 = 30%
30/43 = 70%
● Étape 3 : Faire un tableau d'effectif théorique.
▼X Y►
Père né en France
Père né à l'étranger
Marge de X
Mère née en France
(146x142) / 189 = 110
(146x47) / 189 = 36
146
Mère née à l'étranger
(142 x 43) / 189 = 32
(47x43) / 189 = 11
43
Marge de Y
142
47
N = 189

● Étape 4 : Faire un tableau de contribution.
▼X Y►
Père né en France
Père né à l'étranger
Mère née en France
(129-110) ² /110 = 3,3
(17-36) ² /36 = 10
Mère née à l'étranger
(13-32) ² /32 = 11,3
(30-11) ² /11 = 32,8
A partir de la, trois calculs possibles :
► Le Khi-deux : (noté X²) somme de toutes les contributions.
Calcul : 3,3 + 11,3 + 10 + 32,8 = 57,4
► Le V de Cramér : X² / N x (min (L,C)-1)
Calcul : 57.4 / 189 x (2-1) = 0.3
On en déduit l'intensité du lien entre les variables :
0.0<...<0.3 lien faible
0.3<...<0.5 lien moyen
0.5<...<1.0 lien fort
► Le coefficient de Phi : X² / N
_____________________________________________
Cas particulier :
Pour les variable quantitatives continues, les modalités sont réunies en classes, appelées « classes
modales ». Ainsi nous avons :
xi
ni
ci
ni x ci
ni x(ci)²
Ni
di
ai
modalité
effectif
Centre de la classe
densité
amplitude
ni/ai
Exemple :
[1.8;2.5[
11
(1,8 + 2.5) /2 =
2,5
27,5
68,75
11
7.7
2.5-1.8 =
0,7
[2.5;3[
25
(2.5+3) /2 =
2,75
68,75
189
36
12.5
3-2.5 =
0.5
[3;3.5[
32
(3 + 3.5) /2 =
3,25
104
338
68
16
3.5-3 =
0.5
Définitions de notions de vocabulaire technique :
• vocabulaire de base :
– population : ensemble sur lequel porte l'étude (exemple ici dans l'enquête : résidents en
France avec une condition sur l'âge entre 14 et 35 ans=> condition pour faire partie de l'enquête)

– individu : élément de la population. (exemple : ici une personne, mais peut être un pays, des
animaux... en fonction du contexte)
– échantillon : partie de la population pour laquelle on a observé un certain nombre de
caractères, ou des variables (âge, sexe...)
– taille de l'échantillon : nombre d'individu dans l'échantillon (exemple : ici échantillon 189
personnes, la taille = 189)
– variable : le caractère étudié sur l'échantillon, la population (exemple : « nom de ville »)
– modalités : ensemble des valeurs observées pour un caractère, une variable (exemple : ici 42
modalités différentes pour 42 villes différentes)
• variables :
A) variables quantitatives : on va les utiliser le plus souvent.
> se qu'on appel variables quantitative, c'est une variable dont les modalités sont des quantités. Pas
seulement des chiffres qui codent les réponses.
Exemple : âge, nombre de colocataires...
> distinction à faire entre 2 sous-types :
– variables quantitatives discrètes : ce sont des variables dont l'ensemble des modalités est
comptable (dénombrable). Ce n'est pas tout un spectre continu de possibilités.
Exemple : tous les « nombre de... » , les notes...
– variables quantitatives continues : ce sont les variables dont l'ensemble des modalités n'est
pas dénombrable.
→ si on avait la précision « infinie » deux individus distincts auraient toujours 2 modalités
distinctes.
Remarque : une variable quantitative est continue si la moyenne de n'importe quel échantillon est
une modalité qui aurait pu être prise par un individu. Idée = taux de natalité par exemple, 2,1
enfants /foyer dans un pays=> les femmes mais on peut pas avoir 2,1 enfant ! Par entre l'âge ou la
taille c'est possible.
En pratique on utilise pour simplifier des classes.
Exemple : pour les âges [20,21[ la variable « âge » désigne l'ensemble des âges comprit entre 20 et
21 ans. (Ici 20 inclus, 21 exclus). En général on se ramène à des nombre entiers.
B) variables qualitatives :
> variables dont les modalités ne sont pas des quantités
exemple : « sexe », « nom de ville »...
> distinction à faire entre 2 sous-types :
– qualitative ordinale : les modalités peut être ordonnées de manière naturelle.
– qualitative nominale : les modalités ne sont pas ordonnées.
Chapitre 2 : exercices relatifs à la partie 1.
• organisation des données :
Définition : on appel effectif le nombre de fois où elle apparaît dans les données brutes.
A) tableau d'effectifs et fréquences
On va se servir de cet effectif pour dresser un tableau qui est « un tableau d'effectifs et de
fréquences ».
On va partir des données brutes, pour aller vers un tableau qui sera une représentation synthétique.
Exemple : ici 189 données brutes, variables.
Notation mathématiques : on note x1, x2... xn (nombre de modalités) les différentes
modalités apparaissant pour une variable X donnée (ou classe). Pour chaque modalités xk
(n'importe laquelle des modalités de la liste), on note Nk l'effectif correspondant.

Tableau d'effectifs :
« Xi » ce qui code une modalité
« Ni »
x1
n1
x2
n2
...
...
Xn
Nn
total
N
[N= taille de l'échantillon]
propriété : la somme des effectifs est égal à la taille de l'échantillon n1+n2+...Nn = N
exemple : « quartier idéal »
modalités
effectifs
1
13
2
24
3
56
4
63
5
33
TOTAL
189
Définition : le fréquence d'une modalité xk c'est la quantité Fk=Nk/N (la fonction Fk) (Nk effectif
de xk)
propriété : F1+...Fn = 1
définition : l'information contenue dans le tableau d'effectifs ou de fréquences est appelée
distribution empirique.
B) regroupement de modalités
trop de modalités différentes → on fait des classes.
>si la variable est quantitative les classes seront des intervalles (exemple : [20,21[ )
>si la variable est qualitative les classes seront les catégories
exemple : pour « nom de ville » on peut regrouper les 42 modalités en « Toulouse » et « hors de
Toulouse ».
Les variables quantitatives continues utilisent nécessairement des classes !!!!
exercice 2.
TD n°2 de statistiques du 12.02
exercices 3 et 4
Partie 2 : représentations graphiques seulement des variables qualitatives
rappel de la dernière fois : on a eu les définitions, 4 types de variables, méthodes pour les