Le hasard pour approcher le nombre π http://www.pratiquemath.org

0
1
0
1
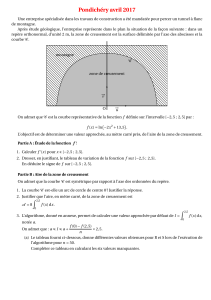
Figure 1
Figure 2
Le hasard pour approcher le nombre π
ππ
π
http://www.pratiquemath.org/spip/spip.p
Mise en situation surprenante.
En faisant appel au hasard nous allons déterminer avec une « certaine » précision une valeur
approchée du nombre PI. PI est le nombre par lequel il faut multiplier le diamètre d'un cercle pour
obtenir la longueur de sa circonférence. La notation du nombre PI a été choisie au XVIIIème
siècle, et correspond à la première lettre du mot grec signifiant « périmètre ». Depuis plus de 4000
ans, les mathématiciens ont constaté que PI n'était pas un nombre « ordinaire ». Il est impossible
de connaître sa valeur exacte en écriture décimale ou fractionnaire ... La valeur de Pi est
aujourd'hui approchée avec une très grande précision. Voici les 51 premières décimales de PI :
3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105
Le nombre de décimales connues se compte en milliards, avec une évidence, les chiffres de toute
écriture approchée du nombre PI ne font apparaître aucune succession logique entre eux.
Aussi il est étonnant qu’en faisant appel « au hasard » on puisse « approcher » une telle valeur
numérique. Le procédé est d’autant plus intéressant qu’il n’est pas limité à la seule approche du
nombre PI. En mathématique, toute approche d’une valeur numérique relevant d’une simulation
fondée sur « le hasard » est dite méthode de Monte-Carlo (en référence aux jeux de casino). Le
grand avantage des méthodes de Monte-Carlo, bien que moins performantes que d’autres faisant
appel à des « outils mathématiques » plus élaborés, est de ne nécessiter que le calcul du quotient
« nombre de cas favorables sur le nombre de cas possible », ce qui est très simple. Ces
méthodes sont aujourd’hui de plus en plus utilisées en physique des particules, en économie,
dans l’étude des risques, en physique médicale, …
Exemple de simulation pour déterminer une valeur approchée de PI : http://jpq.pagesperso-
orange.fr/proba/montecarlo/index.htm
Étude
Les figures ci-contre représentent
un carré de côté 2 dans lequel est inscrit un
carré de diagonale 2
un carré de côté 2 circonscrit à un cercle de
rayon 1.
Le rapport entre l’aire de la surface interne par
rapport à l’aire du grand carré s’exprime par :
carré grand du aire
interne surface la de aire
Pour conduire l’étude cela considérons que
- chacune des deux figures ci-contre représente une cible.
- on lance des fléchettes qui toutes atteignent leur cible
- l’impact de la flèche est « au hasard » (on dit « aléatoire » qui fait référence à la fonction
ALEA(°) du tableur).
Ainsi, chaque flèche lancée atteint :
 un point du grand carré extérieur à la surface hachurée
OU BIEN
 un point de la surface hachurée

-1
-0,5
0
0,5
1
-1 -0,5 0 0,5 1
Cas de la figure 1
La probabilité qu’une flèche atteigne le carré inscrit est égale à 2/4 soit à 0,5
Question 1 : Expliquer et justifier l’affirmation « La probabilité qu’une flèche atteigne le
carré inscrit est égale à 2/4 soit à 0,5 ».
Cas de la figure 2
Pour traiter la situation donnée par la figure 2, on choisit de
modéliser le lancer de fléchettes avec un tableur.
Principe de la modélisation : l’impact résultant de chaque
« lancer au hasard » d’une fléchette est représenté par un point du
carré pouvant ou non se situer dans le disque.
Pour désigner chacun de ces points d’impact on peut imaginer un
repère du plan comme indiqué sur la figure. Ainsi, chaque point
d’impact de fléchette est défini par un couple de coordonnées :
l’abscisse comprise entre -1 et 1
l’ordonnée entre -1 et 1.
On peut simuler un lancer au hasard d’une fléchette « en tirant au sort » un couple de nombres,
chacun pris de 0 à 1, l’abscisse et l’ordonnée de ce point dans le repère imaginé.
La simulation peut être mise en place sur une feuille de calcul du tableur : on commande dans
deux cellules le tirage au sort un nombre entre -1 et 1 :
- la valeur dans la première représente l’abscisse d’un point d’impact
- la valeur dans la deuxième représente son ordonnée.
Le tableau ci-dessous et la figure ci-contre rend
compte de la simulation de 39 lancers de
fléchettes.
On remarque que l’aire du grand carré est 4 et que
l’aire du disque est π
ππ
π. De là, en utilisant les
résultats de la simulation (voir tableau des valeurs)
on en déduit une valeur approchée de π
ππ
π :
π
ππ
π = 3,1794871
Question 2 :
Compléter le tableau ci-dessous puis décrire les
étapes du raisonnement et des calculs qui
conduisent à la valeur approchée de π
ππ
π trouvée
à partir de cette simulation. Justifier.
0
1
1
-
1
-1

Tableau des valeurs de la simulation sur tableur
N° des
impacts abscisse ordonnée distance au centre
Impact situé
dans le disque
1 -0,8957 0,7423 1,1633 NON
2 0,4997 0,0113 0,4998 OUI
3 -0,3408 -0,9592 1,0179 NON
4 0,6076 0,1748 0,6322 OUI
5 0,4812 0,4774 0,6778 OUI
6 0,5601 0,6852 0,8849 OUI
7 -0,0723 -0,6968 0,7005 OUI
8 0,6451 0,9781 1,1716 NON
9 0,4734 0,3231 0,5731 OUI
10 0,7759 -0,5274 0,9381 OUI
11 0,5524 0,425 0,6969 OUI
12 0,9572 0,2029 0,9784 OUI
13 -0,3973 -0,9767 1,0544 NON
14 -0,3574 -0,6255 0,7204 OUI
15 0,5395 0,0815 0,5456 OUI
16 0,2403 -0,779 0,8152 OUI
17 0,3013 0,9348 0,9821 OUI
18 0,9721 0,2097 0,9944 OUI
19 -0,2893 -0,0011 0,2893 OUI
20 0,0471 0,0571 0,074 OUI
21 -0,2256 -0,8368 0,8666 OUI
22 -0,8176 -0,8874 1,2066 NON
23 0,0033 0,1176 0,1176 OUI
24 -0,5706 -0,7091 0,9101 OUI
25 0,943 0,654 1,1475 NON
26 -0,6114 0,5861 0,8469 OUI
27 0,5037 -0,5819 0,7696 OUI
28 -0,3801 -0,0693 0,3863 OUI
29 0,3701 0,4429 0,5771 OUI
30 0,4651 -0,5831 0,7458 OUI
31 -0,5376 0,7627 0,9331
32 0,8941 0,1946 0,915
33 0,1163 -0,7671 0,7758
34 0,7683 -0,4412 0,8859
35 -0,5691 0,9677 1,1226
36 0,9792 -0,1887 0,9972
37 -0,6541 -0,7996 1,033
38 -0,6123 -0,7027 0,932
39 0,1022 -0,6995 0,7069