Angle Un angle est une figure géométrique formée de deux demi

Manuel de l’élève,p.166
4.1
© 2005, Les Éditions CEC inc. • Reproduction autorisée
Nom :
Groupe : Date :
16 Panorama 4
Angle
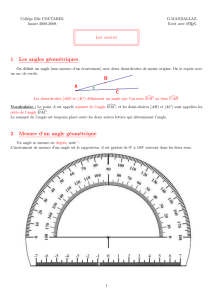
Un angle est une figure géométrique formée
de deux demi-droites ayant la même origine. L’origine
des demi-droites est le sommet de l’angle et les deux
demi-droites sont les côtés de l’angle.
On indique généralement l’ouverture de l’angle
par un arc de cercle.
On nomme généralement un angle par son sommet. S’il
y a risque de confusion, on utilise alors trois lettres. La let-
tre située au centre représente le sommet de l’angle. On
peut aussi utiliser un nombre pour identifier un angle.
On utilise parfois des symboles pour alléger l’écriture :
•«∠» signifie «angle»;
•«m ∠» veut dire «mesure de l’angle».
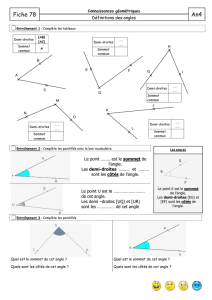
On mesure l’ouverture d’un angle à l’aide d’un instrument
appelé le rapporteur. L’unité de base pour mesurer
des angles est le degré.
Pour construire un angle, voir l’Album, p. 232.
Sommet
Arc
Angle
Côté
Côté
Notation
A
C
B
1
m ∠A = 35°
ou
m ∠BAC = 35°
ou
m ∠1 = 35°
On classe les angles selon leur mesure.
Angle nul Angle aigu Angle droit Angle obtus
mesure = 0°0°< mesure < 90°mesure = 90°90°< mesure < 180°
Angle plat Angle rentrant Angle plein
mesure = 180°180°< mesure < 360°mesure = 360°
Ex. : La mesure de cet angle
est 35°.
*CALEPINS_Panorama 8/22/05 10:32 AM Page 16

Manuel de l’élève,p.167
4.1
© 2005, Les Éditions CEC inc. • Reproduction autorisée
Nom :
Groupe : Date :
17
Panorama 4
Transformation géométrique
Une transformation géométrique permet d’associer, à toute figure initiale, une figure image.
Si un point de la figure initiale est identifié par A, alors le point homologue de la figure image
est noté A' (se lit «A prime»).
Rotation
La rotation est une transformation géométrique qui permet d’associer, à toute figure initiale,
une figure image selon un centre, un angle et un sens de rotation donnés.
•On utilise le symbole rpour désigner une rotation.
•Le centre de rotation est un point fixe.
•L’angle de rotation est une mesure
en degrés qui peut être représentée
par une flèche de rotation.
•Il existe deux sens de rotation :
horaire () et antihoraire ().
On peut indiquer ce sens en attribuant
un signe àl’angle de rotation. Le signe
positif correspond au sens antihoraire et
le signe négatif au sens horaire.
A
A'
C
C'
B
B'
P
Figure
initiale
r
Figure
image
Flèche de
rotation Centre
de rotation
La rotation est une transformation qui permet d’obtenir des figures isométriques, c’est-à-dire
que la figure image a la même forme et les mêmes dimensions que la figure initiale.
Des figures isométriques sont parfaitement superposables.
Le symbole «≅» signifie «est isométrique à». Par exemple, pour indiquer que le triangle ABC
est isométrique au triangle A'B'C', on écrit ∆ABC ≅∆A'B'C'.
Pour tracer l’image d’une figure par une rotation, voir l’Album, page 233.
Le triangle A'B'C' est l’image
du triangle ABC par la rotation r
de centre P et d’angle –60°.
*CALEPINS_Panorama 8/22/05 10:32 AM Page 17