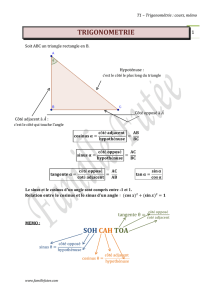
Exercice n°1 - Inspiré du brevet Métropole Septembre 2009 La

Troisième – 31750 – Géométrie –Trigonométrie - Brevet – 13.11.12 http://www.soutienpedagogique.com
Exercice n°1 - Inspiré du brevet Métropole Septembre 2009
La figure ci-dessous représente un cône de révolution d’axe (OH).
On donne   
Dessiner le triangle HOM en vraie grandeur.
Dessinons la base du cône en vraie grandeur.
Calculer la longueur HM et donner le résultat arrondi au mm près.
On verse de l’eau dans le cône jusqu’au quart de sa hauteur.
Quel pourcentage du volume total du cône est occupé par l’eau ?
Exercice n°2 - Inspiré du brevet Groupe Sud Juin 2006
Construire un triangle ABC rectangle en C tel que   
Calculer la longueur BC arrondie au mm près.
Où se trouve le centre O du cercle circonscrit au triangle ABC. Tracer ce cercle.
En déduire la mesure de l’angle 
Exercice n°3 - Inspiré du brevet Métropole Juin 2007
Les longueurs sont exprimées en mètres.

Troisième – 31750 – Géométrie –Trigonométrie - Brevet – 13.11.12 http://www.soutienpedagogique.com
Exercice n°4 - Inspiré du brevet Métropole Juin 2007
Exercice n°5 - Inspiré du brevet Métropole Juin 2007
Exercice n°6 - Brevet Métropole Juin 2011
La figure ci-dessous représente une figure géométrique dans laquelle on sait que :
ABC est un triangle rectangle en B. CED est un triangle rectangle en E.
Les points A, C et E sont alignés. Les points D, C et B sont alignés. AB = CB = 2 cm. CD = 6 cm.
1. Représenter sur la copie la figure en vraie grandeur.
2. a. Quelle est la mesure de l’angle 
 ? b. En déduire la mesure de l’angle   ?
3. Calculer une valeur approchée de DE à 0,1 cm près.
4. Où se situe le centre du cercle circonscrit au triangle DCE ? Tracer ce cercle, que l’on notera Ω puis tracer
Ω’ le cercle circonscrit au triangle ABC.
5. Les cercles Ω et Ω’ se coupent en deux points : le point C et un autre point noté M. Les points D, A et M
sont-ils alignés ?
Si le travail n’est pas terminé, laisser tout de même trace de la recherche. Elle sera prise en compte dans la
notation.

Troisième – 31750 – Géométrie –Trigonométrie - Brevet – 13.11.12 http://www.soutienpedagogique.com
Exercice n°1
Dessinons le triangle HOM et la base du cône en vraie grandeur à l’aide d’un rapporteur, en sachant qu’il est
rectangle en H, que  
. A l’aide d’un compas, on a la distance du rayon du cercle égale à
HM.
Calculons la longueur HM.
Nous connaissons la longueur    qui est la longueur du côté adjacent de l’angle 
On cherche HM la longueur du côté opposé à cet angle.
La fonction trigonométrique qui relie le côté opposé et le côté adjacent d’un angle est la fonction tangente.
Calculons le pourcentage du volume total du cône occupé par l’eau si on verse de l’eau cône jusqu’au quart de
sa hauteur.
En versant de l’eau à l’intérieur du cône, on obtient un petit cône rempli d’eau à l’intérieur du grand. Ce petit
cône est obtenu avec un coefficient de réduction de ¼. On a donc l’égalité suivante en terme de volumes :
Le pourcentage du volume du cône occupé par l’eau est donc égal à :

Troisième – 31750 – Géométrie –Trigonométrie - Brevet – 13.11.12 http://www.soutienpedagogique.com
Exercice n°2
Construisons un triangle ABC rectangle en C tel que   
Calculons la longueur BC.
Nous connaissons la longueur    qui est la longueur du côté adjacent de l’angle 
On cherche BC la longueur du côté opposé à cet angle.
La fonction trigonométrique qui relie le côté opposé et le côté adjacent d’un angle est la fonction tangente.
Cherchons où se trouve le centre O du cercle circonscrit au triangle ABC.
Le cercle circonscrit à un triangle rectangle a pour diamètre son hypoténuse. Son centre est donc le milieu de
cette hypoténuse.
Le centre O du cercle circonscrit au triangle ABC est le milieu du segment .
Déduisons-en la mesure de l’angle 
Les angles 
 interceptent le même arc de cercle  . L’angle   est l’angle au centre, et l’angle 
est l’angle inscrit.

Troisième – 31750 – Géométrie –Trigonométrie - Brevet – 13.11.12 http://www.soutienpedagogique.com
Exercice n°3
Calculons HI
Comme ABIE est un carré, on a :     
Comme B, I et H sont alignés, on a :              
Calculons HE
Comme ABIE est un carré, on a :     
Utilisons le théorème de Pythagore sur le triangle EIH.
Calculons la mesure de l’angle 
 :
Méthode 1 : nous connaissons la longueur    qui est la longueur du côté opposé de l’angle 
 et la
longueur    qui est la longueur de l’hypoténuse.
La fonction trigonométrique qui relie le côté opposé et l’hypoténuse d’un angle est la fonction sinus.
Méthode 2 : nous connaissons la longueur    qui est la longueur du côté opposé de l’angle 
 et la
longueur    qui est la longueur de l’hypoténuse.
La fonction trigonométrique qui relie le côté opposé et l’hypoténuse d’un angle est la fonction sinus.
Méthode 3 : nous connaissons la longueur    qui est la longueur du côté opposé de l’angle 
 et la
longueur    qui est la longueur du côté adjacent.
On cherche HM la longueur du côté opposé à cet angle.
La fonction trigonométrique qui relie le côté opposé et le côté adjacent d’un angle est la fonction tangente.