Espaces affines euclidiens

Espaces affines euclidiens - orthogonalité
Activité 1 : définitions des espaces affines orthogonaux
On rappelle qu’un espace vectoriel euclidien  est un espace vectoriel muni d’un produit scalaire
euclidien. Pour tout sous-espace vectoriel  d’un espace vectoriel euclidien , on définit l’espace
orthogonal comme suit : = ∈  |∀ ∈  ∶ (, )= 0}
On démontre alors les propriétés suivantes :
()= 
 ⊂  ⇒ ⊂ 
( + )= ∩  et ( ∩ )= + 
En s’appuyant sur ces connaissances, lire les pages 27 et 29 du poly de Chris Peters « Géométrie –
DKMAT 368» et traiter les exercices 3.1, 3.2, 3.5, 3.6, 3.9 et 3.10
Activité 2 : définition des réflexions et bissectrices
Lire les pages 29 et 30 du poly de Chris Peters « Géométrie – DKMAT 368» et traiter les exercices
3.12, 3.13 et 3.16.
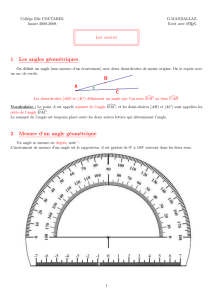
Activité 3 : quelques définitions d’angles ou mesures d’angles
Angles non orientés de vecteurs (définition par la mesure de l’angle)
Soient A,B,C trois points d’un espace affine euclidien . On appelle angle non orienté des
vecteurs  et  et on note 
 le nombre réel  = ((
,  )).
Angles de demi-droites (définition par une relation d’équivalence)
Deux demi-droites [O,x) et [O,y) de même origine O définissent un secteur angulaire saillant
noté [xOy] : c’est l’intersection des demi-plans de frontière (O,x) et contenant [O,y) et de
frontière (O,y) contenant [O,x).
Définition : Soient D et D’ deux demi-droites de même origine O, munies de repères normés
(O,I) et (O,J) (c’est-à-dire OI=OJ=1). Pour tous points distincts M et N de D on note M’ et
N’ leurs projetés orthogonaux sur D’. Alors le rapport c (D, D’ ) =  est indépendant de M et
de N est appelé rapport de projection orthogonale de D sur D’
Définition : Dans l’ensemble des secteurs angulaires saillants, on définit la relation ℜ par :
[xOy] ℜ [x’O’y’] ⟺ c[,),[,)= c,,,.
Théorème : ℜ est une relation d’équivalence. Les classes d’équivalences sont appelées,
angles géométriques. On note 
 l’angle dont un représentant est [xOy].
Bissectrice d’un secteur angulaire.
Théorème : Il existe une unique réflexion  échangeant les deux côtés d’un secteur angulaire
donné [xOy] .La demi-droite Δ ∩ []est appelée bissectrice du secteur angulaire [xOy] . De
plus cette bissectrice est l’ensemble des points de ce secteur équidistants à ses côtés.

Activité 4 : démonstrations du théorème de Pythagore
Définition : Soient D et D’ deux demi-droites de même origine O, munies de repères
normés (O,I) et (O,J) (c’est-à-dire OI=OJ=1). Pour tous points distincts M et N de D on note
M’ et N’ leurs projetés orthogonaux sur D’ . Alors le rapport c (D, D’ ) =  est indépendant
de M et de N est appelé rapport de projection orthogonale de D sur D’ .
Remarque : c (D, D’ ) ∈[−1; 1] et réciproquement, pour tout c ∈[−1; 1] , il existe deux demi-
droites de même origine D et D’ telles que c (D, D’ ) = c.
Théorème : Le rapport de projection orthogonale est symétrique. C’est-à-dire que pour tout
couple de demi-droites de même origine D et D’ : c (D, D’) = c (D’, D)
1) Démontrer ce théorème en utilisant le théorème de Thalès
Théorème de Pythagore sens direct: Pour tout triangle ABC rectangle en A, on a =
+  . Autrement dit « le carré de l’hypoténuse, vaut la somme des carrés des deux
autres côtés ».
2) Démontrer ce théorème en utilisant les rapports de projections orthogonales
Réciproque : Si = +  alors le triangle ABC est rectangle en A.
3) Démonstration de la réciproque :
a) Montrer que ,  et  ne peuvent pas être alignés
b) Considérer ’ le point dans le demi-plan ne contenant pas  tel que ’ =  et
’ est rectangle en . Montrer que  = ’.
c) En déduire que  est le milieu de ’ et conclure.
4) Démontrer le théorème de Pythagore et sa réciproque en utilisant le produit
scalaire.