Pondichéry 2015. Enseignement spécifique

Pondichéry 2015. Enseignement spécifique
EXERCICE 1 (4 points) (commun à tous les candidats)
Partie A
Soit fla fonction définie sur Rpar
f(x)= 3
1+e−2x.
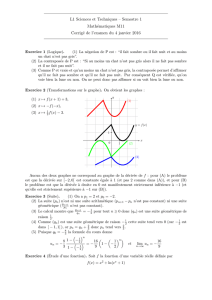
Sur le graphique ci-après, on a tracé, dans un repère orthogonal !O, −→ i,
−→j",lacourbereprésentativeCde la fonction
fet la droite ∆d’équation y=3.
1
2
3
1234−1−2−→ i
−→j
C
∆
1) Démontrer que la fonction fest strictement croissante sur R.
2) Justifier que la droite ∆est asymptote à la courbe C.
3) Démontrer que l’équation f(x)=2,999 admet une unique solution αsur R.
Déterminer un encadrement de αd’amplitude 10−2.
Partie B
Soit hla fonction définie sur Rpar h(x)=3−f(x).
1) Justifier que la fonction hest positive sur R.
2) On désigne par Hla fonction définie sur Rpar H(x)=−3
2ln #1+e−2x$.
Démontrer que Hest une primitive de hsur R.
3) Soit aun réel strictement positif.
a) Donner une interprétation graphique de l’intégrale %a
0
h(x)dx.
b) Démontrer que %a
0
h(x)dx =3
2ln &2 1+e−2a'.
c) On note Dl’ensemble des points M(x;y)du plan défini par (x!0
f(x)"y"3.
Déterminer l’aire, en unité d’aire, du domaine D.
http ://www.maths-france.fr 1 c ⃝Jean-Louis Rouget, 2015. Tous droits réservés.

Pondichéry 2015. Enseignement spécifique
EXERCICE 1 : corrigé
Partie A
1) Pour tout réel x,1+e−2x>1.Enparticulier,pourtoutréelx,1+e−2x̸=0.Parsuite,lafonctionfest dérivable
sur Ren tant qu’inverse d’une fonction dérivable sur Rdont le dénominateur ne s’annule pas sur R.Deplus,pour
tout réel x,
f′(x)=3×−!1+e−2x"′
(1 + e−2x)2=−3×(−2x)′e−2x (1 + e−2x)2=−3×−2e−2x (1 + e−2x)2=6e−2x (1 + e−2x)2.
Pour tout réel x,6e−2x
(1 + e−2x)2>0.Ainsi,lafonctionf′est strictement positive sur Ret donc la fonction fest
strictement croissante sur R.
2) lim
x→+∞
e−2x= lim
X→−∞
eX=0.Parsuite, lim
x→+∞
f(x)= 3
1+0 =3.Onendéduitqueladroite∆est asymptote à la
courbe Cen +∞.
3) Soit x∈R.
f(x)=2,999 ⇔3
1+e−2x=2,999 ⇔1+e−2x=3 2,999 ⇔e−2x=3 2,999 −1
⇔e−2x=0,001
2,999 ⇔−2x= ln #0,001 2,999$⇔x=−1 2ln #0,001 2,999$
⇔x=1
2ln #2,999 0,001$⇔x=1 2ln(2999).
Donc, l’équation f(x)=2,999 admet une unique solution dans Ràsavoirα=1
2ln(2999).Lacalculatricefournit
α=4,00301 ... et en particulier
4<α<4,01.
Partie B
1) D’après la partie A, la fonction fest strictement croissante sur Ret lim
x→+∞f(x)=3.Parsuite,pourtoutréelx,
f(x)<3ou encore, pour tout réel x,h(x)>0.
2) Puisque pour tout réel x,1+e−2x>0,lafonctionHest dérivable sur Ret pour tout réel x,
H′(x)=−3
2×!1+e−2x"′ 1+e−2x=−3 2×−2e−2x 1+e−2x=3e−2x 1+e−2x.
D’autre part, pour tout réel x,
h(x)=3−3
1+e−2x=3+3e−2x−3 1+e−2x=3e−2x 1+e−2x=H′(x).
Ceci montre que la fonction Hest une primitive de la fonction hsur R.
3) Soit aun réel strictement positif.
a) La fonction fest continue sur le segment [0,a]et pour tout réel xde [0,a],f(x)!3.Parsuite,%a
0
h(x)dx =
%a
0
(3 −f(x)) dx est égale à l’aire, exprimée en unités d’aire, du domaine du plan compris entre la courbe Cet la
droite ∆d’une part, les droites d’équations respectives x=0et x=ad’autre part.
http ://www.maths-france.fr 1 c ⃝Jean-Louis Rouget, 2015. Tous droits réservés.

1
2
3
1234−1−2−→i
−→j
C
∆
a
b) %a
0
h(x)dx =[H(x)]a
0=#−3
2ln !1+e−2a"$−#−3 2ln !1+e0"$=3 2!ln(2) −ln !1+e−2a""=3 2ln #2 1+e−2a$.
c) L’aire demandée est lim
a→+∞%a
0
h(x)dx.Or, lim
a→+∞
e−2a=0et donc
lim
a→+∞%a
0
h(x)dx =3
2ln #2 1+0$=3 ln(2) 2.
L’aire, exprimée en unités d’aire, du domaine Dest égale à 3 ln(2)
2.
http ://www.maths-france.fr 2 c ⃝Jean-Louis Rouget, 2015. Tous droits réservés.