Page 1 Première ES IE2 second degré S1 1 Exercice 1 : (3 points) 1

Première ES IE2 second degré S1
1
Exercice 1 : (3 points)
1) Soit le polynôme f(x) = x² + 8x – 10.
a) Recopier et compléter : x² + 8x = (x + 4)² - ……
b) Quelle est la forme canonique de f(x) ?
2) Attribuer à chacune des fonctions polynômes du second degré sa forme
canonique :
 g(x) = x² + 10x + 1 A 
x + 3
2
² - 1
4
 h(x) = x² + 3x + 2 B (x + 5)² - 24
 i(x) = 2x² + 16x – 5 C 2(x + 4)² - 37
Exercice 2 : (7 points)
a) Résoudre les équations données.
1) 15x² + x – 6 = 0
2) x² - 16x = 0
3) (x + 3)(x – 2) = 13x – 17
4) 9a + 4 = (a + 2)²
5) x² - 3x + 5 = 0
b) Donner la forme factorisée de 15x² + x - 6.
c) Donner la forme canonique de x² - 3x + 5.
Première ES IE2 second degré S2
Exercice 1 : (3 points)
1) Soit le polynôme f(x) = x² + 10x + 27.
a) Recopier et compléter : x² + 10x = (x + 5)² - ……
b) Quelle est la forme canonique de f(x) ?
2) Attribuer à chacune des fonctions polynômes du second degré sa forme
canonique :
 g(x) = -x² - 10x - 27 A 
x + 1
2
² + 3
4
 h(x) = 4x² + 8x - 3 B -(x + 5)² - 2
 i(x) = x² + x + 1 C 4(x + 1)² - 7
Exercice 2 : (7 points)
a) Résoudre les équations données.
1) x² + 2x – 6 = 0
2) (u + 9)(13u – 1) = u + 9
3) 8x²- 5x + 1 = 0
4) (v + 6)² + 25 = 0
5) 4x² - 12x = 0
b) Donner la forme factorisée de x² + 2x – 6.
c) Donner la forme canonique de 8x² - 5x + 1.

Première ES IE2 second degré S1
CORRECTION
2
Exercice 1 : (3 points)
1) Soit le polynôme f(x) = x² + 8x – 10.
a) Recopier et compléter : x² + 8x = (x + 4)² - ……
b) Quelle est la forme canonique de f(x).
2) Attribuer à chacune des fonctions polynômes du second degré sa forme
canonique :
 g(x) = x² + 10x + 1 A 
x + 3
2
² - 1
4
 h(x) = x² + 3x + 2 B (x + 5)² - 24
 i(x) = 2x² + 16x – 5 C 2(x + 4)² - 37
1) a) Comme (x + 4)² = x² + 2x4 + 4² = x² + 8x + 16 alors x² + 8x = (x + 4)² - 16
b) La forme canonique de f(x) est (x + 4)² - 10 - 16.= (x + 4)² - 26
2) On peut développer les formes canoniques et les comparer aux formes développées.
A 
x + 3
2
² - 1
4 = x² + 2x3
2+ 
3
2
² = x² + 3x + 9
4 - 1 4 = x² + 3x + 2 = h(x)
B (x + 5)² - 24 = x² + 2x5 + 5 ² = x² + 10x + 25 - 24 = x² + 10x + 1 = g(x)
C 2(x + 4)² - 37 = 2(x² + 2x4 + 4²) - 37 = 2x² + 16x + 32 - 37 = 2x² + 16x – 5 = i(x)
Exercice 2 : (7 points)
a) Résoudre les équations données.
1) 15x² + x – 6 = 0
2) x² - 16x = 0
3) (x + 3)(x – 2) = 13x – 17
4) 9a + 4 = (a + 2)²
5) x² - 3x + 5 = 0
b) Donner la forme factorisée de 15x² + x - 6.
c) Donner la forme canonique de x² - 3x + 5.
a)
1) On calcule le discriminant :  = 1² - 415(-6) = 1 + 360 = 361 = 19²
Comme  > 0, cette équation admet deux solutions distinctes :
x1 = -1 – 19
30 = - 20 30 = - 2 3 et x2 = -1 + 19 30 = 18 30 = 3 5
L’ensemble des solutions de cette équation est S = 
- 2
3; 3 5.
2) x² - 16x = 0  x(x – 16) = 0
 x = 0 ou x – 16 = 0

Première ES IE2 second degré S1
CORRECTION
3
 x = 0 ou x = 16
L’ensemble des solutions de cette équation est S = {0 ;16}.
Remarque : Pour ce type d’équation, il n’est pas nécessaire de calculer le
discriminant.
3) (x + 3)(x – 2) = 13x – 17  x² -2x + 3x – 6 = 13x - 17
 x² + x – 6 – 13x + 17 = 0
 x² - 12x + 11 = 0
On calcule le discriminant :  = (-12)² - 4111 = 144 – 44 = 100 = 10²
Comme  > 0, cette équation admet deux solutions distinctes :
x1 = 12 – 10
2 = 1 et x2 = 12 + 10 2 = 11
L’ensemble des solutions de cette équation est S = {1 ;11}.
4) 9a + 4 = (a + 2)²  9a + 4 = a² + 4a + 4
 a² + 4a – 9a + 4 – 4 = 0
 a² -5a = 0
 a(a – 5) = 0
 a = 0 ou a = 5
L’ensemble des solutions de cette équation est S = {0 ;5}.
5) x² - 3x + 5 = 0
On calcule le discriminant :  = (-3)² - 415 = 9 – 20 = -11.
Comme  < 0, cette équation n’admet pas de solution réelle.
L’ensemble des solutions de cette équation est vide : S = .
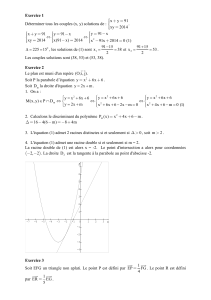
b) La forme factorisée de 15x² + x – 6 est 15 
x + 2
3 
x – 3
5.
c) La forme canonique de f(x) = x² - 3x + 5 est donnée par a(x - )² + β.
avec  = - b
2a et β = f().
Ici a = 1 et b = -3.
Donc  = 3
2 et β = 
3
2
² - 3
3
2 + 5 = 9
4 - 9 2 + 5 = 9 - 92 + 54 4 = 11 4
La forme canonique de x² - 3x + 5 est donc 
x - 3
2
² + 11
4.

Première ES IE2 second degré S2
CORRECTION
4
Exercice 1 : (3 points)
1) Soit le polynôme f(x) = x² + 10x + 27.
a) Recopier et compléter : x² + 10x = (x + 5)² - ……
b) Quelle est la forme canonique de f(x) ?
2) Attribuer à chacune des fonctions polynômes du second degré sa forme
canonique :
 g(x) = -x² - 10x - 27 A 
x + 1
2
² + 3
4
 h(x) = 4x² + 8x - 3 B -(x + 5)² - 2
 i(x) = x² + x + 1 C 4(x + 1)² - 7
1) a) Comme (x + 5)² = x² + 2x5 + 5² = x² + 10x + 25,
Alors x² + 10x = (x + 5)² - 25.
b) La forme canonique de f(x) est (x + 5)² - 25 + 27 = (x + 5)² + 2.
2) On peut développer les formes canoniques et les comparer aux formes développées.
A 
x + 1
2
² + 3
4 = x² + 2x1
2+ 
1
2
² + 3
4 = x² + x + 1 4 + 3 4 = x² + x + 1 = i(x)
B -(x + 5)² - 2 = -(x² + 2x5 + 5²) – 2 = -x² - 10x – 25 – 2 = -x² - 10x – 27 = g(x)
C 4(x + 1)² - 7 = 4(x² + 2x1 + 1²) – 7 = 4x² + 8x + 4 – 7 = 4x² + 8x – 3 = h(x)
Exercice 2 : (7 points)
a) Résoudre les équations données.
1) x² + 2x – 6 = 0
2) (u + 9)(13u – 1) = u + 9
3) 8x²- 5x + 1 = 0
4) (v + 6)² + 25 = 0
5) 4x² - 12x = 0
b) Donner la forme factorisée de x² + 2x – 6.
c) Donner la forme canonique de 8x² - 5x + 1.
a)
1) On calcule le discriminant :  = 2² - 41(-6) = 4 + 24 = 28 = 28² = (2 7)²
Comme  > 0, cette équation admet deux solutions distinctes :
x1 = -2 - 2 7
2 = -1 - 7 et x2 = -2 + 2 7 2 = -1 + 7
L’ensemble des solutions de cette équation est S = {1 - 7 ; 1 + 7}.
2) (u + 9)(13u – 1) = u + 9  13u² - u + 117u – 9 = u + 9

Première ES IE2 second degré S2
CORRECTION
5
 13u² + 116u – 9 – u – 9 = 0
 13u² + 115u – 18 = 0
On calcule le discriminant :  = 115² - 413(-18) = 14 161 = 119²
Comme  > 0, cette équation admet deux solutions distinctes :
x1 = -115 – 119
26 = - 234 26 = - 9 et x2 = -115 + 119 26 = 4 26 = 2 13.
L’ensemble des solutions de cette équation est S = 
-9 ; 2
13 .
3) 8x²- 5x + 1 = 0
On calcule le discriminant :  = (-5)² - 481 = 25 - 32 = -7
Comme  < 0, cette équation n’admet pas de solution réelle.
L’ensemble des solutions de cette équation est vide : S = .
4) (v + 6)² + 25 = 0  (v + 6)² = -25
Or un carré est toujours positif ou nul.
Donc cette équation n’a pas de solution réelle.
L’ensemble des solutions de cette équation est vide : S = .
5) 4x² - 12x = 0  4x(x -3) = 0
 4x = 0 ou x – 3 = 0
 x = 0 ou x = 3
L’ensemble des solutions de cette équation est S = {0 ;3}.
Remarque : Pour ce type d’équation, il n’est pas nécessaire de calculer le
discriminant.
b) La forme factorisée de x² + 2x – 6 est (x – 1 + 7)(x – 1 - 7)
c) La forme canonique de f(x) = 8x² - 5x + 1est donnée par a(x - )² + β.
avec  = - b
2a et β = f().
Ici a = 8 et b = -5.
Donc  = 5
16 et β = 8
5
16
² - 5
5
16 + 1 = 825
256 - 25
16 + 1 = 25 32 - 50 32 + 32 32 = 7 32
La forme canonique de 8x² - 5x + 1 est donc 8
x - 5
16
² + 7
32.