Devoir surveillé N°2.

PCSI. 00/01.
Physique.
Devoir surveillé N°2.
Il est rappelé que votre copie est destinée à être lue et corrigée. En conséquence, une
présentation claire et lisible est recommandée. Il en sera tenu compte dans la notation.
Il est choisi de représenter les vecteurs en caractères gras, non surmontés de flèches. Ainsi le
vecteur sera écrit AB. La valeur du vecteur AB est écrite AB.
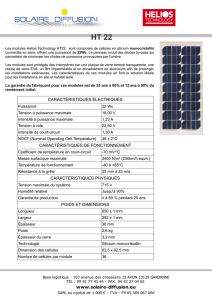
Exercice 1. Utilisation du théorème de Thévenin.
On considère le réseau suivant :
On désire déterminer la tension UCD et pour cela on utilise le théorème de Thévenin.
1. Déterminer la résistance équivalente Req entre C et D.
2. Déterminer la f.é.m équivalente Eeq du générateur de Thévenin pour le circuit ouvert
entre C et D. Pour déterminer cette grandeur on demande d'appliquer le théorème de
Millman successivement aux points A et C.
3. Déterminer l'expression de la tension UCD.
Exercice 2. Lois de composition.
Soit une plaque carrée ABCD, de côté a. On suspend la plaque par deux fils, de même
longueur l, inextensibles, souples, attachés en A et O1 pour le premier et en B et O2 pour le
second. O1 et O2 sont situés sur une même horizontale, distants de a, fixes dans le repère O 1x,
O1y, O1z noté R.
On considère des petites oscillations, de période T, de la plaque, dans le plan vertical contenant
O1O2 caractérisées par l'angle variable  = (O1z, O1A) = ocost avec  = 2/T.
On définit un repère « tournant » de base ur, u, avec :
ur = O1A/O1A, u orthogonal à O1A tel que le trièdre (ur, u, uy) soit direct ( uy unitaire suivant
O1y)
On appelle R1 le trièdre direct (Ax1, Ay1, Az1) lié à la plaque.
1. Donner l'expression de vA/R dans la base de projection (ur, u).
A quels instants tk son module est-il maximal ?
2. Caractériser le mouvement du repère R1 par rapport à R.
En déduire l'expression de vC/R.
3. A l'instant t = 0, un insecte I part du point C et décrit le segment CB avec une vitesse
constante V = -Vuz1 par rapport à la plaque.
Comparer les accélérations a(A) et a(I) par rapport à R.
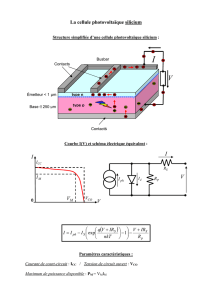
Exercice 3.Conductivité des semi-conducteurs.
1. Mise en évidence de quelques ordres de grandeur.
Pour réaliser du silicium de "type N", on a incorporé à du silicium pur, du phosphore, à raison de
Nn=1,5.1021 atomes de phosphore par m3 de silicium; pour réaliser du silicium de "type P", on a
incorporé à du silicium pur, du bore, à raison de Np = 3,0.1023 atomes de bore par m3 de
silicium; on suppose que les atomes de phosphore ou de bore sont régulièrement répartis dans
le cristal de silicium.
Déterminer :
1.1. Pour le silicium pur le nombre d'atomes par m3.
1.2. Pour un volume donné de silicium de type N le rapport r du nombre d'atomes de
silicium au nombre d'atomes de phosphore.
1.3. La masse m’ de phosphore à incorporer à m = 1 kg de silicium pour obtenir la
concentration Nn, indiquée pour le silicium de type N.
Données :
 les masses atomiques du silicium et du phosphore en g/mol :
Msi = 28 MP = 31
 la masse volumique du silicium  = 2 330 kg.m-3
 le nombre d'Avogadro NA = 6,02.1023 mol-1
2. Calculs de conductivités.
On considère un milieu conducteur homogène dans lequel coexistent 2 types de porteurs de
charge régulièrement répartis :

des porteurs de charge positive +q à raison de p porteurs par m 3

des porteurs de charge négative -q à raison de n porteurs par m3.
Dans ces conditions, V étant le vecteur vitesse moyenne d'un porteur de charge soumis à un
champ électrique E, on définit la mobilité P des porteurs positifs par VP = P E et la mobilité n
des porteurs négatifs par Vn = n E.
2.1. Exprimer la densité de courant j en un point quelconque de ce milieu homogène
soumis à un champ électrique uniforme d'intensité E : en déduire l'expression de la
conductivité  de ce milieu en fonction de q, n, p et des mobilités.
Interpréter.
2.2. Calculer numériquement:
2.2.1. La conductivité n et la résistivité n du silicium de type N en considérant que le
phénomène de conduction y est dû uniquement à la présence de n = N n électrons par
m3 ,ces électrons ayant une charge - q = - 1,6.10- 19 C et une mobilité
n = - 0,15 m2.V-1.s-1.
2.2.2. La conductivité p et la résistivité p du silicium de type P en considérant que le
phénomène de conduction y est dû uniquement à la présence de p = N p porteurs
positifs par m3 ,ces porteurs ayant une charge q = 1,6.10- 19 C et une mobilité p =
0,05 m2.V-1.s-1.
2.2.3. La conductivité i et la résistivité i du silicium à l'état pur en considérant que le
phénomène de conduction y est dû à la fois à la présence de n = n i électrons par m3
et de p = ni porteurs positifs par m3, tous ces porteurs ayant les caractéristiques
précédemment indiquées.
On donne ni =1 ,5.1016 m-3.