Exercice 2 : NOMBRES ENTIERS ET DIVISEURS

CRPE - Mathématiques
Elisabeth Rébillard – Afadec – Droits de reproduction réservés 1
Complément de connaissances
Exercice 2 : NOMBRES ENTIERS ET DIVISEURS MULTIPLES!
Division euclidienne
Il s'agit de la division dans laquelle le dividende, le diviseur, le quotient et le reste sont des
nombres entiers.
Cette division s’écrit à l’aide de l’égalité suivante :
86 = 3 × 28 + 2
« Dans 86, il y a 3 fois le nombre 28 et il reste 2 »
Multiples Diviseurs
Si a et b sont deux entiers naturels, b n'étant pas nul, on dit que :
b divise a
ou que b est un diviseur de a s'il existe un entier q tel que a = bq.!!
ou que a est un multiple de b
Propriétés : p un entier non nul.
si p divise a et b alors il divise a + b ;
si p divise a et a + b, alors p divise b ;
si p divise a, alors p divise a × b.
!
!
!

CRPE - Mathématiques
Elisabeth Rébillard – Afadec – Droits de reproduction réservés 2
Nombres premiers
Définition : Un nombre entier est un nombre premier s'il n'est divisible que par lui-même et
par 1.
Attention : par convention, le nombre 1 n'est pas considéré comme premier.
Exercice 3 : CONSTRUCTION A LA REGLE ET AU COMPAS
Dans certains problèmes, il est demandé de construire la figure à la règle et au compas ; vous
laisserez alors toujours les traits de construction apparents. Rappelez-vous, qu'on utilise
toujours une propriété de géométrie pour ces constructions
Pour tracer la perpendiculaire à un segment donné en un point, prolongez le segment par un
segment de même longueur à l’aide du compas, puis tracez la médiatrice de ce segment.
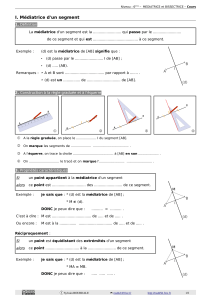
Médiatrice d'un segment [AB]
Dessiner le segment [AB], Tracer les cercles de centres A et B et rayon AB. Tracer les points
C et C', intersections des deux cercles.
Tracer la médiatrice (CC') passant par les deux points d'intersection.
Placer un point M libre sur la médiatrice et vérifier l'égalité des longueurs MA = MB.
Cacher les cercles (non dessinés).
Cette construction permet aussi de trouver à la règle et au compas le milieu d'un segment.

CRPE - Mathématiques
Elisabeth Rébillard – Afadec – Droits de reproduction réservés 3
Exercice 4 : THEOREME DE THALES
Dans les deux cas de figure suivants :
1. On doit calculer une longueur.
Si les droites (BM) et (CN) se croisent en A,
ou si A, B, M, et A, C, N sont alignés,
ou si A ∈ (BM) et A ∈ (CN)
et si (MN)//(BC)
alors, d’après le théorème de Thalès :
!"!
!" = !" !" = !"! !"
2. Les droites (BC) et (MN) sont-elles parallèles ?
On commence par calculer les quotients
!"!
!" et
!"
!" :
⇒ Si
!"!
!" =
!"
!"
et si les deux points des deux droites sont alignés dans le même ordre

CRPE - Mathématiques
Elisabeth Rébillard – Afadec – Droits de reproduction réservés 4
ou si A ∈ [BM] et A ∈ [CN] (figure 1)
ou si N ∈ [AC] et M ∈ [AB] (figure 2)
alors, d’après la réciproque du théorème de Thalès :
les droites (MN) et (BC) sont parallèles.
⇒ Si
!"!
!" ≠
!"
!"
alors, d’après la contraposée du théorème de Thalès :
les droites (MN) et (BC) ne sont pas parallèles.
Exercice 5 : VOLUMES
1 Litre = 1 dm3 donc 1 m3 = 1000 litres
Volume d’un cône : !"²×!
! où R est le rayon du disque et h la hauteur du cône
Un coefficient de réduction est inférieur à 1.
Un coefficient d’agrandissement est supérieur à 1.
Ne pas oublier de mettre ce coefficient au carré pour un calcul d’aire et au cube pour un calcul
de volume.