Le circuit RLC libre et amorti

Le circuit RLC libre et amorti
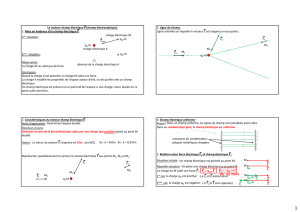
I- Etude expérimentale
1- Production des oscillations libres et amorties
a- Expérience et observations
Après avoir chargé le condensateur (position 1).On bascule l’interrupteur
sur la position 2, on obtient les oscillogramme suivant relatifs à
la tension aux bornes du condensateur et celle aux bornes du résitor
Réaliser l’expérience
b- Interprétation
A l’état d’équilibre, la tension uc aux bornes du condensateur ainsi que sa charge q est nulle. On constate
que l’oscillogramme relatif à uC est symétrique par rapport à l’axe des temps ce qui montre que la charge q
du condensateur varie et change de signe à des intervalles successifs et égaux. La charge q prend au cours
du temps des valeurs alternativement positives et négatives autour de celle prise à l’état d’équilibre (q = 0).
On dit que la charge(q) oscille au cours du temps. La charge q est appelée grandeur oscillante et le circuit
RLC est appelé oscillateur.
Cette décharge se fait d’elle-même, les oscillations sont dites libres. On constate aussi :
*L’amplitude (la valeur maximale) de la tension uc diminue au cours du temps : les oscillations sont alors
amorties ;
* les tensions uc et uR sont presque périodiques, on dit alors qu’elles sont pseudopériodique.
2-Influence de la résistance du circuit
Commencer
i
K
C
R A B
E
uC uR
(1)
(2)
L, r

II- Etude théorique (Le condensateur est chargé et K en (2)
1-Equation différentielle
Loi des mailles :
ub + uR + uc = 0
Loi d’ohm ub = r.i + L
di
dt
et uR = Ri
On a i = C
C
du
dt
et
di
dt
= C
2
2C
du
dt
ub = r.i + L
di
dt
= r. C
C
du
dt
+ L C
2
2C
du
dt
et uR = Ri = R C
C
du
dt
Donc ub + uR + uc = r. C
C
du
dt
+ L C
2
2C
du
dt
+ R C
C
du
dt
+ uc = 0
L C
2
2C
du
dt
+ (R+r) C
C
du
dt
+ uc = 0
2
2C
du
dt
+
(R+r)
L
.
C
du
dt
+
1
LC
uc = 0
2
2C
du
dt
+
1
.
C
du
dt
+
2
0
w
uc =0 avec  =
L
(R+r)
et
0
w
=
1
LC
(pulsation propre de l’oscillateur)
C’est l’équation différentielle relative è uc(t) dont la solution est hors programme
Remarque :L'évolution de la charge du condensateur d'un circuit RLC série est régie en régime libre
par l'équation différentielle
2
2
d
dtq
+
R
L
.
d
dt
q
+
1
LC
. q = 0
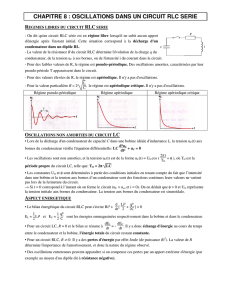
2-Nature d’oscillation
Un circuit RLC série auquel on a transféré initialement de l'énergie peut être le siège d'oscillations
électriques libres amorties, c'est le régime pseudo-périodique
*Régime pseudo périodique et régime apériodique
Les oscillations libres d'un circuit RLC série sont d'autant plus amorties et leur pseudo-période est
d'autant plus grande que la résistance R du circuit est plus grande tout en restant inférieure à une
valeur RC. Pour des valeurs suffisamment élevées de la résistance R, c'est le régime apériodique
3-La non conservation de l’énergie totale de l’oscillateur
Les oscillations libres d'un circuit RLC série sont dues aux transformations mutuelles de ses
énergies électrique et magnétique
En régime libre, l'énergie totale d'un circuit RLC série ne se conserve pas car sa résistance
a- Expression de l’énergie totale E
E = EC + EL avec
EC =
2
C
1C.u
2
c’est l’énergie électrique emmagasinée par le condensateur
EL =
2
1L.i
2
c’est l’énergie magnétique emmagasinée par la bobine
Donc E =
2
C
1C.u
2
+
2
1L.i
2
b- La non conservation de l’énergie totale E
dE
dt
=
22
C
d 1 1
( C.u L.i )
dt 2 2
=
C
Cdu
1 1 di
C.(2.u . ) L.(2.i. )
2 dt 2 dt
=
C
Cdu di
C.u . L.i.
dt dt
(1) (3)
(2)
Régime pseudopériodique Régime apériodique critique Régime apériodique
K
C
R A B
uC uR
(2)
L, r
ub

Or i = C
C
du
dt
dE
dt
=
2
C C C
C2
du du du
C.u . L.C. .C
dt dt dt
=
2
CC
C2
du du
C. (u . L.C )
dt dt
Or d’après l’équation différentielle on a
2
C
C2
du
u . L.C dt
= - (R+r) C
C
du
dt
= -(R+r) i
Donc
dE
dt
= -(R+r) i² < 0 donc l’énergie totale E décroît au cours du temps
Application
Le circuit de la figure -1- comprend :
- Un générateur G de courant d’intensité constante I0 = 0,5 mA.
- Un condensateur de capacité C.
- Une bobine d’inductance L = 0,1 H et de résistance r = 10 Ω.
- Un résistor de résistance R0 = 30 Ω.
- Un interrupteur inverseur K.
1- Le condensateur est initialement déchargé, à l’instant t = 0s, on ferme l’interrupteur K
en position (1).
Donner en fonction de temps les expressions de la charge électrique q accumulée sur
l’armature positive du condensateur et la tension uc à ses bornes.
2- À l’instant t1 on bascule K sur la position (2).
a- Montrer que l’équation différentielle reliant la tension uC aux bornes du condensateur et ses
dérivées est
L C
2C
2
du
dt
+ (R0 + r).C
C
du
dt
+uC = 0
b- Exprimer l’énergie totale Etot du circuit (R0+ r, L, C) en fonction de L, C, uC et i.
c- Montrer que cette énergie décroît au cours du temps.
3- Un dispositif approprié permet de visualiser à partir de l’instant t 1, la courbe
donnant la variation au cours du temps de la tension uC aux bornes du condensateur et
correspondante à la figure-2-
Energie
Temps
Energie totale
EC EL
L,r
I0
K
C
(1)
(2)
R0
A B
Figure -1-
Figure-2-
t(s)
t = 0,03 s
12
8
uC(V)
t1
0
Figure-2-

a- Déterminer la tension uC à l’instant ou on a basculé K sur la position (2)
b- De quel régime s’agit-il ? Justifier la réponse.
c- Déterminer la pseudo période T des oscillations de la tension uC aux bornes du condensateur
d- La résistance totale du circuit étant faible, on admet que la pseudo période T est
égale à la période propre T0 de l’oscillateur (L,C) déterminer la capacité C du
condensateur et déduire l’instant t1
e- Déterminer la variation de l’énergie du circuit entre les instants t1 et t1+ 3T..
f- Déduire que cette énergie décroît au cours du temps et déterminer l’énergie perdue entre t1 et t1+ 3T
Correction
1- L’interrupteur K en position (1)
q = I0.t Puisque le courant qui circule dans le circuit est constant.
uc =
q
C
=
0
I .t
C
2- À l’instant t1, on bascule K sur la position (2)
a- D’après la loi des mailles, on a uR0 + ub + uC = 0.
avec uR0 = R0.i et ub = r.i + L
di
dt
ce qui nous donne
R0.i + r.i + L
di
dt
+ uC = L
di
dt
+ (R0 + r).i + uC = 0
or i =
C
du
dq C
dt dt
di
dt
=
2C
2
du
Cdt
On déduit alors que L
2C
2
du
Cdt
+ (R0 + r).
C
du
Cdt
+ uC = 0 qui est l’équation différentielle relative
à la tension uC
b- L’énergie totale Etot = EL + EC avec EL=
1
2
.L.i² (L’énergie magnétique de la bobine) et
EC =
1
2
.
2
C
Cu
(L’énergie électrique emmagasinée dans le condensateur)
Donc Etot =
1
2
.L.i² +
1
2
.
2
C
Cu
c-
tot
dE
dt
=
1
2
.L.2.i.
di
dt
+
1
2
.C.2.uC.
C
du
dt
= L.i.
di
dt
+. C.uC.
C
du
dt
= or i =
C
du
Cdt
di
dt
=
2C
2
du
Cdt
donc
tot
dE
dt
= L.
C
du
Cdt
.
2C
2
du
Cdt
+ C.uC.
C
du
dt
= C.
C
du
dt
(L.
2C
2
du
Cdt
+ uC).
D’après l’équation différentielle L.
2C
2
du
Cdt
+ uC = - (R0 + r).C
C
du
dt
tot
dE
dt
= - (R0 + r).
2
C
du
Cdt
= - (R0 + r).i² < 0
tot
dE
dt
< 0 et par suite Etot diminue au cours du temps
3-a- On a basculé K sur la position (2) à l’instant t1 donc uC(t1) = 12 V
b- Il s’agit-il du régime pseudo périodique puisqu’on a obtenue des oscillations amorties
c- On a t =3.T = 0,03 s T =
t
3
= 0,01s
d- T = T0 =
2 L.C
T ² =
2
4 L.C
C =
2
2
T
4L
=
-4
2
10
4.(3,14) .0,1
= 25.10-6 F
uC(t1) =
01
I .t
C
= 12 V t1=
C
0
C.u
I
=
-6
-3
25.10 .12
0,5.10
= 0 ;6 s
I0
K
C
(1) A B
uC
L,r
K
C
(2)
R0
A B
i
i
ub
uR0

e- La variation de l’énergie dans le circuit entre les instants t1 et t2 = t1+ 3T est
On a Etot = EL + EC =
1
2
.L.i² +
1
2
.
2
C
Cu
Etot = EL + EC =
1
2
.L.i² +
1
2
.
2
C
Cu
Etot = Etotfinal - Etot initial = Etot (t2) - Etot (t1)
Etot (t1) = EL(t1) + EC(t1) =
1
2
.L.i²(t1) +
1
2
.
2
C1
C u (t ) 
or pour t = t1 uC est max donc i(t1) =0
Etot (t1) =
1
2
.
2
C1
C u (t ) 
de même pour t = t2 uC est max Etot (t2) =
1
2
.
2
C2
C u (t ) 
Etot =
1
2
.
2
C2
C u (t ) 
-
1
2
.
2
C1
C u (t ) 
=
1
2
.
22
C 2 C 1
C (u (t ) - u (t ))
=
1
2
25.10-6 (8²-12²) = -10-3J
L’énergie perdue dans le circuit es 0,4 J
f- Etot < 0 donc il s’agit d’une perte d’énergie
L’énergie perdue est |Etot| = 10-3J