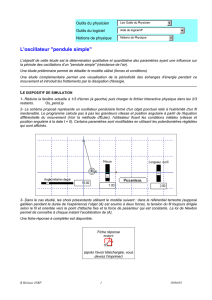
L`oscillateur élastique horizontal

B Richoux INRP 1 19/06/03
Outils du physicien Les Outils du Physicien
Outils du logiciel Aide du logiciel IP
Notions de physique Notions de Physique
L'oscillateur élastique horizontal
L'objectif de cette étude est la détermination qualitative et quantitative des paramètres ayant une influence sur
la période des oscillations d'un "pendule élastique" horizontal en l'absence de tout frottement (support ou
résistance de l'air).
Une étude préliminaire permet de détailler le modèle utilisé (forces et conditions)
Une étude complémentaire permet une visualisation de la périodicité des échanges d'énergie pendant ce
mouvement.
LE DISPOSITIF DE SIMULATION
1- Réduire la fenêtre actuelle à 1/3 d'écran (à gauche) puis charger le fichier Interactive physique dans les 2/3
restants.
Os_elas.ip
2- Le schéma proposé représente un oscillateur horizontal formé d'un objet reposant sans frottement sur un
plan, relié à l'extrémité d'un ressort. Le programme calcule pas à pas les grandeurs vitesse et position à partir
de l'équation différentielle du mouvement (Voir la méthode d'Euler), l'utilisateur fixant les conditions initiales
(vitesse et position à la date t = 0). Certains paramètres sont modifiables en utilisant les potentiomètres
réglables qui sont affichés.
3- Dans le cas étudié, les choix préexistants utilisent le modèle suivant : dans le référentiel terrestre (supposé
galiléen pendant la durée de l'expérience) l'objet (A) est soumis à tois forces, la tension du ressort qui est
proportionnelle à l'élongation du ressort mais toujours de signe contraire, la réaction du support qui est normale
à ce dernier en l'absence de frottement et la force de pesanteur qui est constante.La loi de Newton permet de
connaître à chaque instant l'accélération de (A).
Une fiche-réponse à compléter est disponible.
Fiche réponse
(après l'avoir téléchargée, vous
devrez l'imprimer)

B Richoux INRP 2 19/06/03
L'oscillateur élastique horizontal ( I )
L'OBJECTIF DE L'ACTIVITÉ
Une étude préliminaire permet de détailler le modèle utilisé (forces et conditions)
TRAVAIL PRÉLIMINAIRE SUR LE MODÈLE
1. Lancer la simulation (bouton Exec) : compléter le schéma dans
le compte-rendu en représentant les vecteurs forces selon la
position de (A). Trouver la position de repos du système en fixant la
valeur de l'abscisse initiale à 0. Noter la définition de l'élongation.
Le mouvement s'effectue de part et d'autre de la position d'équilibre
matérialisée par l'axe vertical bleu. Cette position correspond au
ressort au repos (ni étiré ni allongé) ce que l'on constate quand
l'abscisse initiale est nulle.
L'élongation est l'abscisse du centre d'inertie de (A) quand l'origine
du repère est justement la position d'équilibre statique du système.
La tension du ressort est toujours opposée à l’élongation
2. Observer le diagramme [2] : que signifie-t-il ?
Quel est le paramètre qui est ainsi visualisé ?
Décrire les opérations de calcul qui permettent
l'affichage de ce graphe.
Le graphe [2] signifie que le modèle de tension
utilisé par la simulation est bien une force
proportionnelle à l'élongation.
Cette droite de coefficient directeur négatif
indique que cette tension est toujours opposée à
l'élongation .
Le calcul qui permet cet affichage est décrit dans les étapes suivantes, selon la méthode d'Euler.
Le pas du calcul sera noté δt, l'accélération a étant donnée par la loi de Newton qui se réduit ici à :
T (t) = m a(t) - k x(t) = m x"(t)
On Vérifie que les calculs d'une ligne sont possibles car tous les termes qui y figurent sont calculés dans les
lignes précédentes.
Les conditions initiales sont, avec m = 1 kg et k = 100 N/m :
x(0) = x0 = 0,5 et v(0) = v0 = x'(0) = 0
t = 0
x0
v0
a0 = T0 / m = - (k/m) . x0
t = t1
x1 = x0 + δt . v0
v1 = v0 + δt . a0
a1 = T1 / m = - (k/m) . x1
t = t2
x2 = x1 + δt . v1
v2 = v1 + δt . a1
a2 = T2 / m = - (k/m) . x2
et ainsi de suite...

B Richoux INRP 3 19/06/03
3. Observer le diagramme [1] : les opérations du
calcul précédent permettent-elles l'affichage de ce
graphe ? En déduire une méthode de mesure de la
période de la courbe visualisée.
Les élongations x(t) sont calculées par la méthode
d'Euler (voir la page précédente) et le graphe est
construit pas à pas.
La courbe obtenue est apparemment une
sinusoïde dont on peut mesurer la période : il
faut utiliser l'affichage de la date et repérer sur
le graphe le passage du point représentatif à la
même élongation et dans le même sens.(utiliser
le mode d'affichage pas à pas )
L'oscillateur élastique horizontal ( II )
L'OBJECTIF DE L'ACTIVITÉ
L'objectif de cette étude est la détermination qualitative et quantitative des paramètres ayant une influence sur
la période des oscillations d'un "pendule élastique" horizontal en l'absence de tout frottement (support ou
résistance de l'air).
Influence des paramètres
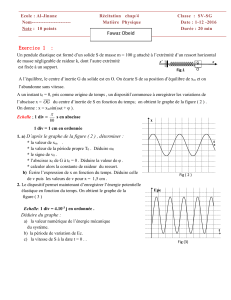
1. Lancer la simulation (bouton Exec) avec les
valeurs suivantes pour les paramètres affichés :
m = 1 kg k = 100 N/m x(0) = 0,45 m
Pesanteur : terrestre
La période dans les conditions de référence est :
6 Tref = 3,768 s soit Tref = 0,628 s
2. Modifier successivement chaque paramètre (un seul à la fois bien sûr) pour étudier leur influence sur la
période, sans oublier de revenir au réglage initial entre chaque étude. Résumer vos résultats et interprétations
dans le tableau de la fiche réponse.
Influence de la masse
on modifie la valeur de m et on mesure la période :
masse m en kg période T en s
1 0,628
2 0,888
3 1,09
4 1,26
La période est une fonction croissante de la masse,
elle est multipliée par 2 lorsque la masse est
multipliée par 4 ce qui laisse penser que la relation
entre T et m est du type

B Richoux INRP 4 19/06/03
Influence de la raideur du ressort
On modifie la valeur de k et on mesure la période
:
raideur k en N/m période T en s
50 0,888
100 0,.628
150 0,510
200 0,442
La période est une fonction décroissante de la
raideur k , elle est divisée par 2 lorsque k est
multipliée par 4 ce qui laisse penser que la
relation entre T et k est du type :
Influence de la pesanteur
On modifie la valeur de g en choisissant celle que l'on rencontrerait sur la lune et on mesure la période : ce
changement est sans effet sur la valeur de la période.
Par contre on connaît la modification de la norme des vecteurs "poids" et par conséquent de la réaction normale
du support, ce que l'on vérifie lorsque le vecteur n'est pas trop petit !.
Influence de l'abscisse initiale
On modifie la valeur de x(0) et on mesure la période :
x(0) en m 0,35 0,45 0,60 0,75
période T en s 0,625 0,628 0,628 0,625
La période ne dépend pas la valeur de l'abscisse
initiale : on dit que les oscillations sont
isochrones.
3. En utilisant les équations aux dimensions, établir l'expression de la période des oscillations. Calculer la
constante sans dimension de votre relation en utilisant une valeur numérique prise dans la simulation.
Si on admet que la période ne dépend que des paramètres m et k, on peut écrire l’équation aux dimensions :
Dans les conditions de référence on avait :
Tref = 0,628 s m = 1 kg k = 100 N/m ce qui donne cte = 6,28 valeur proche de 2 π.

B Richoux INRP 5 19/06/03
L'oscillateur élastique horizontal ( III )
L'OBJECTIF DE L'ACTIVITÉ
L'objectif est l'étude de la périodicité des échanges d'énergie pendant les oscillations libres non amorties.
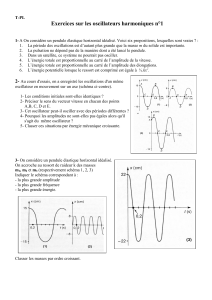
VARIATIONS DES ÉNERGIES EN FONCTION DU TEMPS
1. Les diagrammes énergétiques sont déjà définis. Pour les faire apparaître, il suffit de cliquer dans le bandeau
gauche du graphe.
2. Lancer la simulation avec les réglages de référence.
3. Conclure sur la périodicité des fonctions
représentant les énergies. Etablir ce résultat en
admettant que l'élongation x est de la forme :
La période des énergies cinétique et potentielle
élastique est deux fois plus petite que celle de
l'élongation x.
Période de Ec ou Ep
On rappelle les deux expressions donnant x(t) et la pulsation, ainsi que la définition de Ep :
L'énergie potentielle élastique est :
En utilisant la formule de trigonométrie :
⇒
La pulsation est double et la période sera donc moitié.