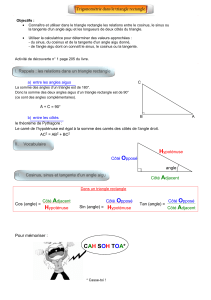
Trigonométrie dans le triangle rectangle

Trigonométrie dans le triangle rectangle.
I) Vocabulaire et définitions
A E
F
B
G
C
Le triangle ABC est Le triangle EFG est
Pour l’angle ACB :
-le côté [BC] est le côté adjacent
-le côté [BA] est le côté opposé
-le côté [AC] est l’hypoténuse.
Pour l’angle GFE :
-le côté [GE] est le côté
-le côté [FG] est le côté
-le côté [FE] est .
Dans un triangle rectangle, pour un angle aigu :
Les formules : Exemples, pour les triangles ci-dessus :
cosinus =
hypoténuseldelongueur
angleldeadjacentcôtédulongueur
'
'
sinus =
hypoténuseldelongueur
angleldeopposécôtédulongueur
'
'
tangente =
angleldeadjacentcôtédulongueur
angleldeopposécôtédulongueur
'
'
II) La trigonométrie à la calculatrice
On connaît l’angle en degré. On peut calculer le cosinus, le
sinus et la tangente de cet
angle.
Avec ma calculatrice :
On connaît le cosinus ou le
sinus ou la tangente d’un
angle.
On peut calculer la valeur de
cet angle en degré.
Avec ma calculatrice :
III) Applications
Les formules de trigonométrie dans le triangle rectangle permettent de :
-de calculer un angle aigu lorsque les longueurs de deux des côtés sont connues
-de calculer la longueur d’un côté lorsqu’un des angles aigus et la longueur d’un côté sont connus.
Evidemment cela demande de bien connaître les noms des côtés par rapport à l’angle considéré et les trois
formules.
Exemple 1.
MNP est un triangle rectangle en N tel que MN= 5cm et MP= 7cm.
Calculer MPN à un degré près.
Exemple 2.

RST est un triangle rectangle en T tel que RT= 4cm et ST= 5cm.
Calculer SRT.
Exemple 3.
IJK est un triangle rectangle en I tel que IJK= 40° et IJ= 3,5cm.
Calculer JK.
Exemple 4.
DEF est un triangle rectangle en F tel que FDE= 65° et FD= 4,4cm.
Calculer FE.
IV) Relations entre sinus, cosinus et tangente
Relation entre sinus et cosinus : A B
Soit ABC un triangle rectangle en A.
C
E G
Relation entre sinus, cosinus et tangente :
Soit EFG un triangle rectangle en G.
F
V) Valeurs possibles du cosinus, sinus et tangente d’un angle aigu.
Nous savons que dans un triangle rectangle le côté le plus long est l’hypoténuse donc :
cosinus =
hypoténuseldelongueur
angleldeadjacentcôtédulongueur
'
'
et sinus =
hypoténuseldelongueur
angleldeopposécôtédulongueur
'
'
sont
inférieurs à 1 et supérieurs à 0.
Par contre la longueur du côté adjacent et la longueur du côté opposé peuvent être l’une ou l’autre la plus
grande donc :
tangente =
angleldeadjacentcôtédulongueur
angleldeopposécôtédulongueur
'
'
est supérieure à 0 mais n’a pas de limite maximale (une
tangente peut être supérieure à 1).