TP n°=3 : Mesures à l`oscilloscope, résonances

1
Jeudi 10 juin 2010
Chloé BROUZES - Emeline BRUNET, groupe T6 binôme C
Université de Technologie de Compiègne
TP n°=3 : Mesures à l’oscilloscope, résonances
Objectif du TP :
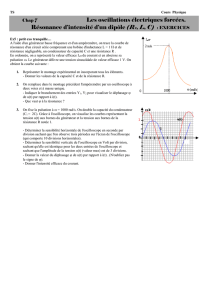
Le but de la manipulation consiste à étudier un circuit RLC afin de tracer d’une part la courbe de résonance de l’intensité, et d’autre part
la courbe de déphasage en fonction de la fréquence.
Matériel utilisé
- un générateur de tension avec un fréquencemètre intégré : Δf = ± 1Hz (la fréquence est affichée à l’unité près)
- un oscilloscope : on ne considère que l’incertitude sur la mesure, soit une demi-graduation
- une bobine d’inductance L = 100 ± 1 mH (car incertitude de 1%)
- un condensateur de capacité variable réglée à   
- une résistance variable réglée à   
Exercice de préparation :
a) Sens de variation du déphasage
Soit 1
  avec ω la pulsation.
La fonction  est dérivable, on a alors ′
Or R, C et L sont positives donc ′ est négative,  est décroissante.
On a  ∅
 or  est décroissante et la fonction tangente est croissante.
∅  est décroissante : le déphasage est une fonction décroissante de la pulsation ω.

2
Jeudi 10 juin 2010
Chloé BROUZES - Emeline BRUNET, groupe T6 binôme C
Université de Technologie de Compiègne
b) Détermination de la bande passante en hertz
On sait que Δω est la bande passante en pulsation, c’est-à-dire une vitesse angulaire en radians par seconde. On cherche à exprimer la
bande passante en hertz, c’est-à-dire une fréquence en « nombre de tours » par seconde.
Un tour par seconde correspond à 2π radians par seconde.
On a donc :    avec   
1. Mesure de la fréquence de résonance de l’intensité
On souhaite mesurer la fréquence de résonance , c’est-à-dire la fréquence pour laquelle le
déphasage entre le courant et l’intensité est nul.
Pour cela, on réalise un montage RLC et on branche l’oscilloscope de manière à pouvoir observer en
voie I la tension entre la sortie du générateur et la masse, et en voie II la tension entre l’entrée de la
résistance et la masse.
Ensuite, on fait varier la fréquence jusqu’à observer un déphasage nul et on relève la valeur de la
fréquence. On effectue 10 mesures afin d’avoir une meilleure précision. On fait la moyenne de nos
10 valeurs, on trouve alors : é  19617
Incertitude sur é :

3
Jeudi 10 juin 2010
Chloé BROUZES - Emeline BRUNET, groupe T6 binôme C
Université de Technologie de Compiègne
 é
On calcule également la valeur théorique de la fréquence de résonance :
ℎ  avec  
 ℎ
Incertitude sur ℎ :
ℎ
ℎ
 ℎ
 ℎ
Commentaires : Notre valeur mesurée est plus faible que la valeur théorique, on peut alors supposer que nous avons fait des erreurs de
lecture, notamment pour  
Cependant nous retrouvons le même ordre de grandeur pour nos
valeurs de résonance sur les courbes qui suivent dans la suite du TP : on peut alors penser que la différence entre théorie et
manipulation est due au matériel.
différence entre nos
valeurs expérimentales et théoriques.

4
Jeudi 10 juin 2010
Chloé BROUZES - Emeline BRUNET, groupe T6 binôme C
Université de Technologie de Compiègne
2. Courbes de l’amplitude et du déphasage de l’intensité
a) Etalonnage de l’oscilloscope
en temps.
 calibrator » 2Vpp afin de vérifier que la tension crête à
scilloscope : le signal affiché ne correspondait pas du tout à
ce que nous aurions dû observer. 
 défaillan qui ne nous a pas permis de réaliser cette étape de la
manipulation. 
b) Courbe de résonance
On va tracer la courbe d’amplitude en fonction de la fréquence sur l’intervalle [0 ; 2fo]. Le montage est réalisé avec une tension de 1.1 V
délivrée par le générateur.
Le montage réalisé permet d’afficher sur l’écran de l’oscilloscope deux courbes de tension : la tension I, correspondant aux dipôles R, L, C
en série, et la tension II, correspondant à la tension aux bornes de la résistance R. Cette tension II nous permet aussi de nous donner
l’allure de la courbe de l’intensité du courant, car d’après la loi d’Ohm on a U résistance = R.I, donc il n’y a pas de déphasage entre la tension
aux bornes de la résistance (tension II) et l’intensité du courant.
Pour chaque valeur de fréquence, on procède comme suit afin de pouvoir relever les tensions I et II, le déphasage, et de déduire
l’intensité I du courant traversant ces dipôles en série.
On commence par régler l’oscilloscope de manière à observer sur l’écran une période, et de façon à obtenir l’origine des deux courbes au
centre de l’écran.

5
Jeudi 10 juin 2010
Chloé BROUZES - Emeline BRUNET, groupe T6 binôme C
Université de Technologie de Compiègne
On relève ensuite pour chaque fréquence la valeur des tensions I et II grâce aux divisons présentes sur l’écran de l’oscilloscope, ainsi que
le déphasage entre ces deux courbes. Nous faisons attention au signe du déphasage, qui correspond à l’avance de phase de l’intensité par
rapport à la tension du générateur.
Une fois la tension II relevée, on peut en déduire la valeur de l’intensité du courant I qui traverse les dipôles R, L, C en série : I =
U(résistance)/R
On obtient donc les valeurs suivantes :
fréquence (Hz)
tension I (V)
tension II (V)
intensité du courant :
I= U(II)/R (mA)
500
0,44
0,04
0,2
700
0,44
0,08
0,4
900
0,44
0,1
0,5
1000
0,44
0,12
0,6
1200
0,44
0,16
0,8
1400
0,42
0,24
1,2
1600
0,414
0,35
1,75
1800
0,38
0,58
2,9
1900
0,36
0,72
3,6
2000
0,36
0,73
3,65
2100
0,36
0,64
3,2
2200
0,39
0,51
2,55
2400
0,4
0,34
1,7
2600
0,42
0,26
1,3
2800
0,42
0,21
1,05