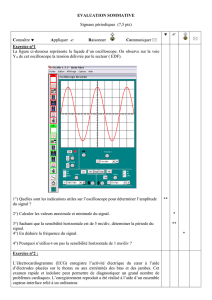
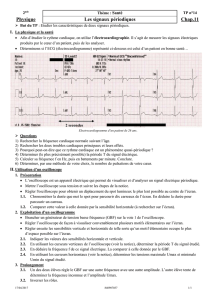
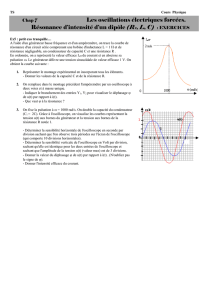
Calcul de la valeur théorique

1
Jeudi 3 juin 2010
Chloé BROUZES - Emeline BRUNET, groupe T6 binôme C
Université de Technologie de Compiègne
TP n°=2 : Oscilloscope à mémoire, décharge d’un condensateur
Objectif du TP :
Nous allons étudier des signaux transitoires et plus particulièrement calculer les
constantes de temps associées à chaque montage. Pour cela nous allons utiliser un
oscilloscope numérique afin de visualiser les signaux
Matériel utilisé
- oscilloscope numérique à mémoire TDS1000 : Δt = 1/25*sec/div et ΔV=1/25*volt/div
- bobine de 1H : ΔL/L = 1%
- une résistance variable de valeur maximale 100kΩ : ΔR/R =1.0%
- une résistance variable de valeur maximale 1kΩ : ΔR/R =0.5%
- une résistance variable de valeur maximale 100Ω : ΔR/R =0.5%
- un générateur de tension
- condensateur utilisé à C=0,02 µF : ΔC/C = 1.0%
Exercice de préparation :
Incertitude sur τ :
A.N :   

2
Jeudi 3 juin 2010
Chloé BROUZES - Emeline BRUNET, groupe T6 binôme C
Université de Technologie de Compiègne
1. Prise en main de l’oscilloscope
L’objectif de cette partie est de se familiariser avec le fonctionnement d’un oscilloscope,
de manière à savoir réaliser des mesures en réglant les différents paramètres d’affichage
de l’oscilloscope.
a) Observation d’un signal périodique :
On observe un signal fourni par l’oscilloscope lui-même. Ce signal est périodique, carré.
- On mesure la période : à l’aide des curseurs, on mesure l’intervalle de temps
entre le début et la fin d’une période : T = 10.0 µs => f=1/T => f=100 kHz
Incertitude sur T :     
Incertitude sur f : 
- On mesure l’amplitude du signal : On observe qu’un signal a une hauteur de 2,50
divisions, or l’oscilloscope est réglé de manière à ce que 1 div  2.00 V. Donc
amplitude = 2.50 * 2.00 = 5.00 V.
Incertitude sur l’amplitude :   
b) Etude du temps de montée
Lorsque qu’on passe à une vitesse de balayage de 1µs/div, on observe que le signal
délivré par l’oscilloscope n’est en réalité pas carré, mais qu’il augmente
progressivement. On cherche à connaître le temps de montée à 95 %, c'est-à-dire à
connaitre le temps que met le signal à atteindre 4.75 V. A l’aide des curseurs de tension
et des curseurs de temps, on trouve qu’il faut 0.920 µs à l’oscilloscope pour atteindre 95
% de sa valeur finale.

3
Jeudi 3 juin 2010
Chloé BROUZES - Emeline BRUNET, groupe T6 binôme C
Université de Technologie de Compiègne
2. Observation de la décharge d’un condensateur dans une résistance – Mesure de la
constante de temps pour une décharge unique
Le but de la manipulation est d’enregistrer une décharge afin de vérifier la loi
exponentielle de décharge d’un condensateur et d’évaluer la constante de temps τ.
On règle donc l’oscilloscope selon les paramètres suivants :
Sensibilité = 1,00 V
Vitesse de balayage = 1,00 ms
Niveau de déclenchement = 4 V
Pente descendante - Mode normal
Pour la manipulation, nous avons choisi E = 8,2 V ; R = 100kΩ et C = 0,02 µF.
- Nous allons calculer τ par une première méthode graphique : à l’aide des
curseurs, nous avons relever sur l’oscilloscope la tension et le temps
correspondant à 6 points de la courbe.
On a la relation suivante :
Donc on trace ln(U) en fonction de t afin d’obtenir une droite dont le coefficient
directeur est proportionnel à τ. La droite est d’équation  , avec
α=1/τ, le coefficient directeur.
Nous avons les valeurs de tension et de temps suivantes pour tracer la courbe :
Temps (ms)
Tension U (V)
Ln(U) (sans unité)
0
8,16
2,09
1
4,8
1,57
2
2,84
1,04
3
1,64
0,49
4
0,84
-0,17
5
0,52
-0,65

4
Jeudi 3 juin 2010
Chloé BROUZES - Emeline BRUNET, groupe T6 binôme C
Université de Technologie de Compiègne
Evolution de ln(U) en fonction du temps pour un circuit RC
On a   1
1 055631798
On calcule l’incertitude sur τ :
On utilise la formule d’incertitude calculée lors de l’exercice préparatoire, en remplaçant
par 2 de nos valeurs :
A.N :
Donc  1798 0
y = -0.5563x + 2.119
R² = 0.9986
-1
-0.5
0
0.5
1
1.5
2
2.5
0 1 2 3 4 5 6
ln(U)
Temps (ms)
Series1
Linear (Series1)

5
Jeudi 3 juin 2010
Chloé BROUZES - Emeline BRUNET, groupe T6 binôme C
Université de Technologie de Compiègne
- Nous allons maintenant calculer τ avec la méthode rapide :
On a   
 avec T le temps correspondant à la moitié de la tension maximale (soit la
tension initiale) et   1
2
On mesure alors T sur l’oscilloscope avec les deux curseurs et on trouve T = 1,280 ms
Incertitude sur T :  
On a alors   1280
1
2 1847.
- incertitude sur τ : 
- Nous allons également calculer la valeur théorique de τ :
On sait que   
Donc  100 103002 106200
Donc τ = 2,00 ± 0.04 ms
Commentaires : Nous trouvons des valeurs pour la constante de temps cohérentes
puisqu’elles sont du même ordre de grandeur que la valeur théorique. De plus la
méthode rapide semble plus précise que la méthode graphique. Il semble alors qu’il ne
soit pas nécessaire de tenir compte de l’impédance de l’oscilloscope. La loi exponentielle
est donc vérifiée.
3. Décharge d’une bobine dans une résistance
Le but de cette partie est de déterminer la constante de temps de façon expérimentale et
d’observer l’influence de la résistance sur la constante de temps.
Nous n’utiliserons dans cette partie que la méthode rapide, comme précédemment, pour
déterminer τ.
On effectue les mesures pour trois valeurs de résistances, on obtient les résultats
suivants :