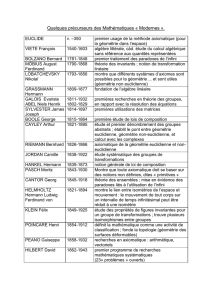
Quelques précurseurs des Mathématiques « Modernes ».

Quelques précurseurs des Mathématiques « Modernes ».
EUCLIDE v. –350 premier usage de la méthode axiomatique (pour
la géométrie dans l’espace)
VIETE François 1540-1603 algèbre littérale, càd. étude du calcul algébrique
sans référence aux quantités représentées
BOLZANO Bernard 1781-1848 premier traitement des paradoxes de l’infini
MÖBIUS August
Ferdinand 1790-1868 théorie des invariants ; notion de transformation linéaire
LOBATCHEVSKY
Nikolaï 1793-1856 montre que différents systèmes d’axiomes sont possibles pour la géométrie ... et sont utiles
(géométrie non euclidienne)
GRASSMANN
Hermann 1809-1877 fondation de l’algèbre linéaire
GALOIS Evariste
ABEL Niels Henrik 1811-1932 1802-1829 premières recherches en théorie des groupes,
en rapport avec la résolution des équations
SYLVESTER James
Joseph 1814-1897 premières utilisations des matrices
BOOLE George 1815-1864 première étude de lois de composition
CAYLEY Arthur 1821-1895 étude et premier dénombrement des groupes
abstraits ; établit le pont entre géométrie
euclidienne, géométrie non-euclidienne, et
calcul avec les complexes
RIEMANN Bernhard 1826-1866 axiomatique de la géométrie euclidienne et non-
euclidienne
JORDAN Camille 1838-1922 étude systématique des groupes de
transformations
HANKEL Hermann 1839-1873 notion générale de loi de composition
PASCH Moritz 1843-1930 Montre que toute axiomatique doit se baser sur
des notions non définies, dites « primitives »
CANTOR Georg 1845-1918 théorie des ensembles ; mise en évidence des
paradoxes liés à l’utilisation de l’infini
HELMHOLTZ
Hermann Ludwig
Ferdinand von
1821-1894 montre le lien entre isométries de l’espace et
mouvement : le mouvement de tout corps sur un
intervalle de temps infinitésimal peut être réduit
à une isométrie
KLEIN Félix 1849-1925 étude des propriétés de figures invariantes pour
un groupe de transformations ; trouve plusieurs
isomorphismes entre groupes
POINCARE Henri 1854-1912 définit la mathématique comme une activité de
classification ; fonde la topologie (géométrie des
surfaces déformables)
PEANO Guiseppe 1858-1932 recherches en axiomatique : arithmétique,
vectoriels
HILBERT David 1862-1943 premier programme de recherches
mathématiques systématiques
(23« problèmes » ouverts)

Découvertes 2
Un siècle de découvertes mathématiques.
* , ** : découvertes considérées comme particulièrement importantes.
Axiomatique, théorie du raisonnement
1895 * Cantor Montre que l’ensemble de tous les ensembles ne peut
exister (par une contradiction dans le calcul de son
cardinal).
1897 Burali-Forti Par un paradoxe ("paradoxe des catalogues"), montre qu’on
ne peut définir en toute liberté des ensembles d’ensembles.
1899 Hilbert Axiomatique complète de la géométrie plane et spatiale,
sans référence à la notion « commune » de points et droites.
Montre que les axiomes de la géométrie euclidienne sont
exempts de contradiction.
1902 ** Russell Crise des fondements de la mathématique, retombée des
travaux de Cantor : une approche naïve des ensembles
infinis et de la notion de définition fait apparaître des
contradictions ; on est obligé de prévoir plusieurs niveaux
de langage mathématique (un pour parler des maths, un
pour parler de celui qui parle des maths etc.), et de refuser
le nom d’ensemble à des collections trop vastes.
Crée avec Whitehead un système logique (théorie des
types) pour obvier à ces contradictions.
1903 Hilbert Montre que les axiomes de certaines géométries non-
euclidiennes (Lobatchevsky) sont exempts de
contradictions.
1905 Richard Par un paradoxe, fait apparaître que toutes les méthodes de
classement des objets mathématiques ne sont pas
nécessairement bonnes.
1908 * Zermelo puis
von Neumann,
Bernays ...
Axiomatique de la théorie des ensembles.
1910 * Zermelo
Enonce l’axiome du choix : étant donné une infinité
d’ensembles, il existe un moyen systématique de
sélectionner un élément dans chacun d’eux ; cet axiome
semble raisonnable et est admis par la majorité des
mathématiciens, mais peut conduire à des paradoxes : des
notions aussi élémentaires que celle de volume deviennent
impossibles à définir correctement.
1913 * Brouwer ... Intuitionnisme : refuse l’axiomatique de la théorie des
ensembles, l’induction infinie, le tiers-exclu, la
démonstration par l'absurde. But : faire des mathématiques
plus proches de l’intuition commune.
1920 Lukasiewicz -
Skolem ... Théorie des modèles : méthodes pour fabriquer une structure répondant à des axiomes donnés.
1924 Tarski Prouve que l’axiome du choix est équivalent à la
proposition : « pour tout a infini, a² = a ».

Découvertes 3
v.1928 Lukasiewicz Principes de la logique floue : admet des énoncés vrais,
faux et partiellement vrais ; très utilisée aujourd’hui en
informatique et en robotique (Zadeh 1965) ; utilisations en
statistique.
1929 Gödel Métathéorème de la complétude : le système logique mis au
point par Russell (cf 1902) peut prouver toute formule vraie
de la logique classique.
1931 ** Gödel Théorèmes d’incomplétude : une théorie suffisamment forte
pour faire de la théorie des nombres (nombres premiers
etc.) ne peut prouver elle-même qu’elle est correcte. Il faut
donc différents niveaux de pensée. Gentzen (1936) prouve
que la démonstration est possible « de l’extérieur ».
1934 Skolem Arithmétique non standard, cohérente avec les axiomes de
Peano ; permet de faire de l’arithmétique avec des entiers
infinis.
1934 Zassenhaus Le « théorème des 4 ensembles », première démonstration
utilisant des diagrammes de Venn («patates»).
1935 Dieudonné -
Chevalley - Weyl... Création du groupe Nicolas Bourbaki, qui tente de faire de la mathématique un tout cohérent par l’usage systématique
de la méthode axiomatique.
1938 Gödel L’hypothèse du continu (il n’y a pas de nombre entre ℵ0 et
C ) est cohérente avec les autres axiomes de la théorie des
ensembles ; l’axiome du choix (voir 1910) aussi.
1961 * Robinson -
Luxemburg Analyse non standard : variante de l’analyse admettant l’existence de nombres infiniment petits. Permet parfois des
démonstrations plus aisées que l’analyse standard (avec
limites et ε).
1963 Cohen La négation de l’hypothèse du continu (il y a des nombres
entre ℵ0 et C ) est cohérente avec la théorie des ensembles;
voir aussi 1938 ; on ne pourra donc jamais démontrer si
l’hypothèse du continu est vraie ou fausse.
1967 Bishop Prouve que la théorie des ensembles « à la Cantor » est
exempte de contradictions, en en construisant un modèle.

Découvertes 4
Structures diverses
1901 * Wilson - Gibbs Axiomatique des vecteurs ; analyse vectorielle (étude de
fonctions dont les variables et/ou les valeurs sont des
vecteurs) ; essentiel en physique (électromagnétisme).
1905 Wedderburn Théorème : si un ensemble est un corps (un groupe
commutatif avec l'addition, un groupe avec la
multiplication et la multiplication distribue l'addition), et
comporte un nombre fini d'éléments, alors c'est un champ
(la multiplication aussi est commutative).
La démonstration fait appel à des sujets aussi variés que :
vectoriels, classes latérales, combinatoire, divisibilité,
polynômes à inconnues dans ∀, plan de Gauss.
1908 * Hensel Théorie des corps p-adiques ; des ensembles de nombres
munis d’une distance aux propriétés inattendues.
1910 Steinitz Axiomatique de l’algèbre ; son cadre naturel est la théorie
des corps (cf 1905 pour la définition).
1914 Fréchet Axiomatique des espaces abstraits, cadre de la topologie, et
des espaces métriques, càd. avec une loi de distance.
1920 Weyl Axiomatique des espaces affins (géométrie avec
parallélisme mais sans mesures).
1934 Löwig Toutes les bases d’un vectoriel ont le même cardinal.
1939 * groupe Bourbaki
(voir axiomatique,
1935)
Définit la mathématique comme l’étude des ensembles
munis d’une structure. En profite pour éditer une œuvre
(encore incomplète !) étudiant systématiquement les
structures.
1941 Albert Théorie des opérations non associatives.
1941 Gel’fand Théorie des algèbres normées, ou vectoriels munis d’une
opération de multiplication interne et d’une distance.
Utilisée en mécanique quantique.
1942 ** Eilenberg - McLane Théorie des catégories : donne une place centrale aux
notions de loi de composition, et de morphisme.

Découvertes 5
Théorie des groupes
1898 Weber Première axiomatique des groupes.
1902 Huntington Axiomes « classiques » des groupes.
1906 Burnside Conjecture que tout groupe simple (càd. n’ayant pas de
sous-groupe invariant) non cyclique est de cardinal pair.
Les groupes simples jouent pour les groupes le même rôle
que les nombres premiers.
1938 Frucht Tout groupe fini est isomorphe au groupe formé des
automorphismes d’un certain graphe (isomorphismes du
graphe avec lui-même), avec la loi usuelle de composition.
1947 Markov - Post Il n’existe pas d’algorithme permettant de déterminer de
manière systématique si deux combinaisons des générateurs
d’un groupe représentent le même élément du groupe
("problème des mots").
1957 * Chevalley -
Steinberg Suzuki - Ri Théorie des groupes simples ; construction utilisant les ressources de la topologie, de l’algèbre des champs finis, du
calcul vectoriel, de la géométrie des pavages, de la théorie
des isomorphismes et des plongements (isomorphismes
entre une structure et une partie d'une autre).
1959 Navikov Construit un groupe infini dont tous les éléments sont
d’ordre fini.
1963 Feit - Thompson Démontrent la conjecture de Burnside (voir 1906).
1972 * Gorenstein Etablit un programme pour la classification des groupes
simples. Ce programme sera achevé en 1980 (voir cette
date) par Aschbacher, Gorenstein, Fischer etc.
1980 Griess - Fischer Construisent un groupe simple de cardinal énorme, le
« monstre », groupe de rotations d’un espace vectoriel de
dimension 196883. Ceci achève la classification des
groupes simples.
1983 Thurston Utilise les groupes d’isométries conservant des figures de
papiers peints pour faire avancer la classification des
surfaces de dimension 3.