Brevet Blanc 2014 » Épreuve de mathématiques

« Brevet Blanc 2014 »
Épreuve de mathématiques
Jeudi 13 février 2014 Durée de l'épreuve : 2 heures
L'emploi de la calculatrice est autorisé.
Toute réponse doit être justifiée.
Tout raisonnement, même non abouti sera valorisé dans la notation.
En plus des points prévus pour chacun des exercices de l'épreuve, la
présentation, la rédaction et l'orthographe seront évalués sur 4 points.
Vous répondrez sur les copies mises à votre disposition et sur l'annexe
de la page 4. N'oubliez pas de rendre l'énoncé avec votre copie.
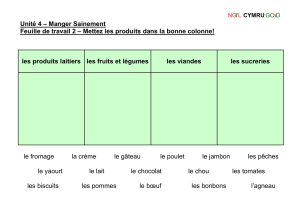
Exercice 1
Un collège de Caen (Normandie) organise un échange avec le Mexique pour les
élèves de 3e qui étudient l'espagnol en seconde langue.
Le tableau ci-dessous permet de déterminer la répartition de la seconde langue
étudiée par les 320 élèves de 4e et de 3e de ce collège.
Seconde langue
étudiée 4e3eTotal
Espagnol 84
Allemand 22 24
Italien 62 50
Total 320
1) Combien d'élèves peuvent être concernés par cet échange?
2) 24 élèves vont participer à ce voyage.
Est-il vrai que cela représente plus de 12% des élèves de 3e ?
Exercice 2
Léa observe à midi, au microscope, une cellule de bambou.
Au bout d'une heure, la cellule s'est divisée en deux. On a alors deux cellules.
Au bout de deux heures, chacune de ces deux cellules s'est divisée en deux.
Léa note toutes les heures les résultats de son observation.
A quelle heure notera-t-elle, pour la première fois, plus de 200 cellules ?
Page 1 sur 4

Exercice 3
On a posé à des élèves de 3e la question suivante :
« Est-il vrai que, pour n'importe quelle valeur du nombre x on a :
5x2 - 10x + 2 = 7x – 4 ? »
•Léa a répondu : « Oui, c'est vrai. En effet, si on remplace x par 3 ,
on obtient : 5 x 32 – 10 x 3 + 2 = 17 et 7 x 3 – 4 = 17 »
•Myriam a répondu : « Non, ce n'est pas vrai. En effet, si on remplace x par 0 ,
on obtient : 5 x 02 – 10 x 0 + 2 = 2 et 7 x 0 – 4 = -4 »
Expliquer pourquoi l'un des élèves a raison et l'autre a tort.
Exercice 4
La pyramide SABCD ci-contre
a pour base le rectangle ABCD
et pour hauteur le segment [SA].
L'unité de longueur est le centimètre.
Rappel :
Volume du cône=Aire de la base×hauteur
3
On donne AB = 8,2 ; AD = 2,3 et SA = 4.
1) Donner, sans les justifier, la nature du triangle SAB et celle du triangle SAD
Dessiner ces triangles en vraie grandeur.
2) Calculer la mesure, arrondie au degré, de l'angle
̂
SBA
.
3) Calculer SD. On donnera la valeur arrondie au millimètre.
4) Calculer la valeur arrondie au
cm3
du volume de la pyramide SABCD.
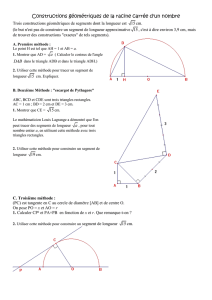
Exercice 5
On considère la figure suivante :
On donne OA = 3,5 cm ; OC = 5 cm ; AB = 2 cm et CD = 3 cm.
1) Expliquer pourquoi les mesures données ci-dessus sont inexactes.
2) Modifier une seule de ces mesures afin que la figure et les autres mesures
indiquées soient cohérentes.
Page 2 sur 4

Exercice 6
Au cours d'une embauche pour la cueillette des pêches, un ouvrier agricole a le
choix entre trois formules de salaire :
Formule A : Un salaire mensuel de 930 €.
Formule B : Une somme mensuelle de 310 € à laquelle on ajoute 40 € par
tonne de pêches cueillies.
Formule C : Un salaire basé uniquement sur la cueillette,
80 € par tonne de pêches cueillies.
1) Sur la feuille annexe, compléter le tableau de valeurs.
2) Si l'on appelle x la quantité de pêches récoltée en tonnes,
exprimer en fonction de x le salaire correspondant à chaque formule.
3) On a représenté sur la feuille annexe les fonctions définies par :
f(x) = 930 et g(x) = 310 + 40 x
Représenter graphiquement, sur cette feuille annexe la fonction h(x) = 80 x
4) a) Pour un mois donné, cet ouvrier agricole gagnerait le même salaire avec
les formules B et C. D'après le graphique, quelle quantité de pêches a-t-il
récolté ? (on laissera apparents les pointillés aidant à la lecture).
b) Répondre par le calcul à la question précédente.
5) a) Par une lecture graphique, préciser la formule la plus avantageuse pour
l'ouvrier s'il espère cueillir 13 tonnes de pêches dans le mois
(on laissera apparents les pointillés aidant à la lecture).
b) Quel sera alors son salaire?
Exercice 7
Le dessin ci-dessous représente
une figure composée d'un carré ABCD
et d'un rectangle DEFG.
E est un point du segment [AD]
C est un point de [DG].
On a toujours AE = 15 cm et CG = 25 cm.
1) Dans cette question on suppose que AB = 40 cm.
a) Calculer l'aire du carré ABCD.
b) Calculer l'aire du rectangle DEFG.
2) Dans cette question, la longueur AB peut varier.
Peut-on trouver la longueur AB de sorte que l'aire du carré ABCD soit égale à l'aire
du rectangle DEFG?
Si oui, calculer AB. Si non, expliquer pourquoi.
Page 3 sur 4
F
GD C
B
A
E

Annexe EXERCICE 6
Question 1
Nombre de tonnes de pêches cueillies dans un mois 5 11 15
Salaire mensuel en euros avec la formule A
Salaire mensuel en euros avec la formule B
Salaire mensuel en euros avec la formule C
Questions 3 ; 4 et 5
Page 4 sur 4
Salaire mensuel (€)
012 3 456 7 8 9 10 11 12 13 14 15 16
Quantité de pêches
(en tonnes)
100
200
300
500
600
400
1000
900
800
700
1100
1200
1300
1400
f(x) = 930
g(x) = 310 + 40x