1 III. COSINUS D`UN ANGLE AIGU 1. Vocabulaire du triangle

4ème-IV-Théorème de Pythagore 1
III. COSINUS D'UN ANGLE AIGU
1. Vocabulaire du triangle rectangle
2. Activité préparatoire : n° 3 p 194
http://mathenpoche.sesamath.net/4eme/pages/geometrie/chap4/serie2/index.html
3. Propriété
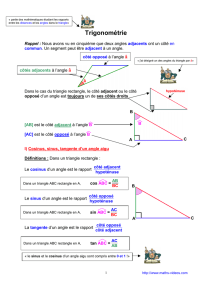
Dans un triangle rectangle, le quotient de la longueur de l’un des côtés de l’angle droit par la
longueur de l’hypoténuse ne dépend que de la mesure de l’angle
4. Définition
Dans un triangle rectangle, le cosinus de l'un des
angles aigus est égal à :
hypoténuseldelongueur adjacentcôtédulongueur '
C'est à dire : Cos BAC = AB
AC
On a aussi : Cos BCA = BC
CA
Remarque
Le cosinus d’un angle aigu est toujours compris entre 0 et 1
Exemples :
Dans le triangle ABC, rectangle en B :
1) Calculer Cos BAC, si AB = 3 cm ; AC = 5 cm et BC = 4 cm :
Cos BAC = BA
AC
Cos
BAC = 3
5 = 0,6
T
Q
A
@options;
@figure;
T = point( 1 , 1 ) { noir };
Q = point( 0.93 , 2.93 ) { noir ,
(-0.43,-0.9) };
L
M
P
@options;
@figure;
L = point( 1 , 1 ) { noir };
M = point( -2.3 , 5.4 ) { noir ,
(-0.43,-0.9) };
Hypoténuse : [QA] Hypoténuse : [MP]
Côté adjacent de
l’angle TQA [QT] Côté adjacent de l’angle LMP [ML]
Côté adjacent de
l’angle TAQ [TA] Côté adjacent de l’angle LPM [LP]
hypoténuse
Côté adjacent
de l’angle
BAC

4ème-IV-Théorème de Pythagore 2
2) Calculer Cos BCA si BCA = 47°
Cos BCA = Cos 47°
Cos BCA = 0,682
5. Applications du cosinus dans un triangle rectangle
a. Calcul de la mesure d'un angle (n° 13 p183)
On calcule la mesure des trois angles du triangle RAS
• RAS : dans le triangle RAS, rectangle en R,
l'hypoténuse du triangle est le côté [AS]
le côté adjacent à l’angle RAS est [RA]
Donc : Cos RAS = RA
AS
Cos RAS = 4,5
5,3
Cos RAS ≈ 0,849
Donc RAS ≈ 32° on utilise la touche Cos
–1
de la calculatrice
Donc l'angle RASmesure 32° (à 1 d° près)
•
ARS : dans le triangle RAS, rectangle en R,
l'hypoténuse du triangle est le côté [AS]
le côté adjacent à l’angle ARS est [SR]
Donc : Cos ARS = SR
RA
Cos ARS = 2,8
5,3
Cos ARS ≈ 0,528
Donc ARS ≈ 58° on utilise la touche Cos
–1
de la calculatrice
Donc l'angle ARSmesure 58° (à 1 d° près)
Remarque :
Pour le calcul de la mesure de ARS, on aurait pu utiliser une autre méthode : la somme des mesures
des angles d’un triangle est égale à 180°
Donc, dans le triangle RAS, rectangle en R :
ARS + RSA + SAR = 180°
ARS + 90° + 32° = 180°
ARS + 122° = 180°
ARS = 180° - 122°
ARS = 58°
EXERCICES

4ème-IV-Théorème de Pythagore 3
b. Calcul de la longueur d'un côté de l'angle droit (n°11 p183)
Soit ABC un triangle rectangle en B tel que BAC = 55° et AC = 6 cm.
Calculer AB (arrondir au mm)
Réponse :
Dans le triangle ABC, rectangle en B,
- l’angle connu est BAC
- le cosinus de cet angle fait intervenir : [BA] et [AC]
Donc Cos BAC = BA
AC
Cos 55° = BA
6
Avec le produit en croix, on a : BA × 1 = 6 × Cos 55°
BA ≈ 6 × 0,574
BA ≈ 3,4 cm
Donc BA est égale à 3,4 cm (au mm près)