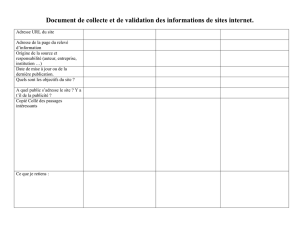
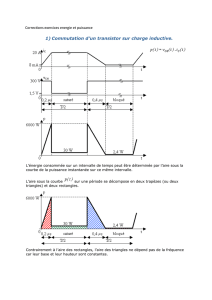
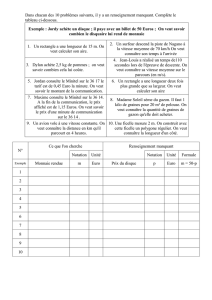
Aires 64 - Les leçons de mathématiques à l`oral du CAPES 2013

9
Aires
64
Leçon n°
Niveau Collège - Terminale S (Intégrale et aire)
Prérequis quadrilatère, fonctions
Références [60], [164], [165], [166], [167], [168]
64.1 Comparer les aires
64.1.1 Egalité d’aires
Définition 64.1 On dit que deux figures ont la même aire si en découpant l’une d’entre elle, on peut
recomposer l’autre.
Exemple 64.2 La figure F1et F2ont la même aire car si on découpe le triangle AE00D00 de la figure
F2et qu’on le place sur l’arrête [DE]de sorte que [DE]et [D00E00]coïncide, on retrouve la figure F1.
F1
A B
C
F2
A B
DE
D00
E00
F1
F2
A B
C
64.1.2 Transformer l’aire d’une figure en celle d’un rectangle
Proposition 64.3 On peut toujours découper un polygone en un rectangle de même aire.
Exemple 64.4 Dans le parallélogramme ABCE, on a découpé le triangle AEO qu’on a collé sur le
segment CB. On obtient ainsi le rectangle OECT .
A B
CE
O
P
B
CE
O
P
T
Proposition 64.5 — Découpage de Dudeney (1902). On peut découper un triangle équilatéral en
quatre morceaux pour qu’il puisse former un rectangle.

10 Leçon n°64 •Aires
Dv
On va expliciter la construction de Dudeney. On se donne un triangle ABC équilatéral de côté 2.
On note Eet Dles milieux de [AC]et de [AB]. On construit Isur [BC]tel que EI4= 3. Pour
cela,
— On construit Mle symétrique de Apar rapport à (BC). Ainsi AM = 2√3.
— On construit le cercle (C2)de centre Mpassant par B, donc de rayon 2. On note Pl’inter-
section de la droite (AM)et du cercle (C2),Pse trouvant à l’extérieur du triangle ABC.
— On note Qle milieu de [AP ]et on construit (C1)le cercle de centre Qpassant par A((C1)
a pour rayon 1 + √3).
— On note Ol’intersection du cercle (C1)et de la parallèle à (BC)passant par M. On a alors
OM = 2 4
√3.
— Soit Nle milieu de [OM]alors MN est la longueur EI cherchée.
On note Fle projeté orthogonal de Dsur [EI]et Gle point de [EI]tel que EG =IF .Hest
l’antécédent sur [BC]de Gpar projection orthogonale sur (EI).
On donne une suite d’instructions à faire sur Geogebra pour réaliser la construction précé-
dente :
A = (0,0)
B = (2,0)
Cercle[A,2]
Cercle[B,2]
C = Intersection[c,d,1]
Polygone[A,B,C]
D = MilieuCentre[A,B]
E = MilieuCentre[A,C]
# Construction du point I
M = Symétrie[A,a]
C_2 = Cercle[M,2]
Droite[A,M]
P = Intersection[e,C_2,2]
Q = MilieuCentre[A,P]
C_3 = Cercle[Q,A]
Droite[M,a]
O = Intersection[C_3,f,1]
N = MilieuCentre[O,M]
Segment[M,N]
Cercle(E,g)
I = Intersection(a,h)
# Fin de la construction du point I
Segment[E,I]
Perpendiculaire[D,h]
F = Intersection[i,h]
Segment[I,F]
Cercle(E,j)
G = Intersection[h,p]
Perpendiculaire[G,h]

64.1 Comparer les aires 11
H = Intersection[a,l]
Segment[G,H]
Segment[D,F]
A B
C
E
D
M
P
Q
O
N
I
F
G
H
64.1.3 Inégalité
Définition 64.6 On dit que deux figures n’ont pas la même aire si en essayant de découper une des
figures pour la reconstituer en l’autre figure, les deux surfaces ne sont pas superposables a.
a. c’est-à-dire qu’une des deux surfaces « dépassent » l’autre
Exemple 64.7 Dans la figure ci-dessous, les deux figures n’ont pas la même aire car si on les
superpose, la surface d’une des deux figures dépassent l’autre.
A B
C
E F
GH

12 Leçon n°64 •Aires
A B
C
F
GH
64.1.4 Les multiples
Définition 64.8 Soit A1(resp. A2) l’aire de deux polygones P1(resp. P2). On dit que les deux aires
sont multiples l’un de l’autre s’il existe k∈Ntel que A1=kA2.
Exemple 64.9 La figure ci-dessous nous montre deux figures dont les aires sont multiples.
A
B
C
E
F
G
64.1.5 Les partages
Définition 64.10 Soit un polygone Pet Ason aire. On dit qu’on partage le polygone Pen des
polygones (P1, . . . , Pn)avec aires (A1, . . . , An)si pour tout 1≤i≤n,Pi⊂P(les polygones Pi
sont dans le polygone P) et il existe 0< ki<1, tels que Ai=kiAet Pn
i=1 ki= 1.
Exemple 64.11 Soit ABCD le rectangle de la figure ci-dessous. On dit que (P1, . . . , P7)partage le
rectangle.
A B
CD E
F
G
H
I
J
P1
P2
P3
P4P5
P6
P7

64.2 Mesurer une aire 13
64.2 Mesurer une aire
64.2.1 Principe
Définition 64.12 — Aire d’une surface. L’aire d’une surface est la mesure de sa surface, dans une
unité d’aire donnée.
Définition 64.13 Mesurer une aire d’un polygone, c’est compter le nombre de carré unité (on préci-
sera l’unité plus tard) qui sont inscrit dans ce polygone.
64.2.2 Méthode
Définition 64.14 On se donne un polygone et un carré unité. Pour calculer l’aire de ce polygone, il
faut le partager avec autant de carré unité que l’on peut (quitte à ce que la surface de ce carré dépasse
la figure).
Définition 64.15 On se donne un polygone et un carré unité. Pour calculer l’aire de ce polygone, on
peut le découper pour en faire un rectangle et ensuite compter le nombre de carré unité inscrit dans
le rectangle.
Exemple 64.16 L’aire du triangle ABC de la figure ci-dessous est 6car en le découpant, on peut
former un rectangle qui contient 6carré unité DEF G.
A
B
C
D E
FG
64.3 Calculer une aire
64.3.1 Aire d’un rectangle
Définition 64.17 — Aire d’un rectangle. Un rectangle de longueur Let de largueur la pour aire L×l.
Dv
•Démonstration — Soit un rectangle de longueur Let de largueur l. Sur la longueur, on peut
inscrit Lcarré unité et sur la largueur, lcarré unité. Donc, le nombre de carrés unité qu’on
peut inscrire dans le rectangle est Ll et ainsi, l’aire du rectangle est Ll. •
Exemple 64.18 L’aire du rectangle de la figure ci-dessous est de 8.