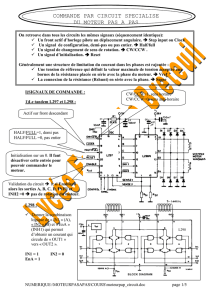
Exercice 1 Exercice 2 Capteur Grandeur physique (onde de

Piste de correction – attention, les réponses ne sont pas rédigées !
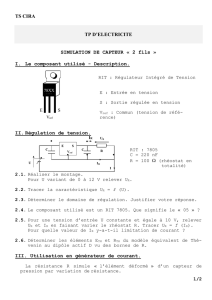
Exercice 1
Q1. Capteur à US
Q2.
Q3. Piézoélectricité
Q4. La période du signal sinusoïdal est T=1/f=1/50000 soit T= 20μs. La durée d'un train est τ = 100 μs. On trouve donc τ/T=100/20=5
périodes de sinusoïdes le train d'ondes.
Q5. La distance maximale dmax de mesure est égale à la moitié de la distance D parcourue par l'onde entre deux trains.
D=vus.T0=340x80.10-3=27,2m donc dmax=13,6 m.
Q6. La distance minimale dmin de mesure est égale à la moitié de la distance D' correspondant à la durée τ du train d'ondes.D'=vus. Τ=
340x 100x10-6=0,034 m donc dmin=0,017 m= 1,7 cm.
Q7. Pour un temps de retour tR=24 ms d= 340x24x10-3/2=4,08 m
Exercice 2
C05 - exercices TSTI2D 5
Capteur
Grandeur physique
(onde de pression)
grandeur électrique
(tension)

Exercice 3
La courbe d’étalonnage d'un capteur est donnée ci-dessous.
1. grandeurs d’entrée = température grandeur de sortie =résistance
2. Il manque les unités : °C pour la température et ohm pour la résistance.
3. C'est une thermistance.
4. Pour θ=40°C : R= 295 ohm et θ=115°C : R=55 ohms .
Une partie du schéma électrique du capteur est donnée ci-contre :
5. Le « transducteur » de ce capteur est entouré.
6. « CTN » signifie coefficient de température négatif.
7. On applique la loi d'Ohm :
V+= Rθ.i
Vcc= (R + Rθ).i
d'où : i = Vcc / (R + Rθ) et donc : V+= Vcc .Rθ/ (R + Rθ)
Exercice 4
Q1.Le signal est non sinusoïdal mais périodique.
Q2. T = 0,08 s donc f= 12,5 Hz
Q3. C'est un spectre obtenu avec la fonction FFT appliquée à la courbe en fonction du temps.
Q4. Ce sont des harmoniques.
Q5. Ils ont le même fondamental, donc le son est de même fréquence. Mais leurs harmoniques sont différents, le timbre ne sera
donc pas tout à fait le même.
Exercice 5
1. Les sons audibles s'étendent de 20 à 20 000 Hz soit 20kHz. D'après le théorème de Shannon, la fréquence d'échantillonnage
doit être au minimum le double de la fréquence maximale du signal, soit 2 x 20 000 = 40 000 Hz. Cela est bien cohérent
avec l’échantillonnage des CD à 44,1 kHz.
2. La voix humaine est comprise dans une bande de fréquence comprise entre 100 et 3400 Hz. La fréquence d’échantillonnage
fe doit être telle que : fe= 2fmax = 2 x 3400 = 6800 Hz.
Exercice 6
1. Taigu = 10-4 s et Tgrave = 10-2 s.
2. Si FE = 1 kHz alors TE = 10-3 s
3. Pour le son grave, chaque période est décomposée en 10 échantillons
Pour le son aigu, dans un échantillon, il y a 10 périodes donc l’information du son aigu est perdue.
Exercice 7
Le CAN d'entrée d'une carte d'acquisition possède les caractéristiques suivantes : Gamme 0 à 5,12V
10 digits
1. Nmax =(2n-1) x Ve / Vref avec Ve = Vref . Soit Nmax =(2n-1) = (210-1) = 1023
C05 - exercices TSTI2D 6

2. tension pleine échelle = 5,12 V
3. Résolution q = Vref / (2n-1)= 5,12 / (210-1)= 5,00.10-3 V = 5,00 mV
4. Valeur numérique (en binaire) de la mesure d’une tension de 4,5 V : ADU =(2n-1) x Ve / Vref =(210-1) x 4,5 /5,12 =899
Exercice 8
Pour l’équipement des salles de chimie du lycée, on a besoin de cartes d'acquisition pouvant mesurer des tensions allant de 0 a 4,5V
a 10mV près. Le modèle le moins cher trouve dans le commerce contient un CAN 8 bits de calibre 5,0V.
1. Résolution q = Vref / (2n-1)= 5,0 / (28-1)= 2,0.10-2 V = 20 mV
2. non, il faudrait une carte 2 fois plus précise.
3. On veut q = 10 mV = 1,0.10-2 V . Soit : q = Vref / (2n-1) 2n = Vref /q + 1 = 5,0/1,0.10-2 + 1 = 501
Pour trouver n, on utilise la fonction logaritme népérien ln :
ln (2n ) = ln(501)
n ln (2) = ln(501)
n = ln(501) / ln (2) = 6,22 / 0,69 = 8,96 = 9
Il faut 9 digits.
Exercice 9
Q1. F : force (grandeur physique) ; ue,us tensions (grandeurs électriques) ; N : nombre binaire (grandeur numérique)
Q2. α= ue/m=50/10 soit α=5 mV/kg ;
Q3. ue= α.m et us=20xue=20x αxm= 20x5x0,2 soit us=20 mV
Q4. usmax= 20x αxm=20x5x100=10000 mV soit usmax=10 V
Q5. q= Δ Vemax /2n où Δ Vemax est la pleine échelle de sortie du CAN et n est le nombre de bits q=10/28 soit q≈39 mV .
Rappel: cela signifie que si la tension à l'entrée du CAN passe, par exemple, de 0 à 30 mV ce dernier donne 0 en sortie ! Il faut
franchir ce seuil de 39 mV pour obtenir une incrémentation d'une unité en sortie du CAN.
D'après Q3., q=20xαxΔm → Δm= q/(20α) =39/(20x5)=0,39 kg ou Δm= 390 g
Q6. Nmax=255 sur 8 bits. Donc u'smax =255xq=255x39=9945 mV ou u'smax≈ 9,9 V.
mMAX= u'smax/(20α)=9945/(20x5) soit mMAX≈ 99,5 kg
Q7. 195 g= Δm/2 ; il faudrait donc un quantum deux fois plus petit ; ceci est obtenu avec 2 fois plus de valeurs codées par le CAN
c'est à dire avec 1 bit de plus !
Exercice 10
1. Avec une quantification de 16 bit (soit une séquence binaire de 16 zéros ou un), on dispose de 216 = 65536 valeurs
pour traduire l’amplitude du signal dans chaque échantillon.
2. Même question avec une quantification de 8 bit (soit une séquence binaire de 8 zéros ou un).
On dispose de 28 = 256 valeurs seulement pour traduire l’amplitude du signal dans chaque échantillon.
Plus la quantification est grande, plus l’amplitude du signal numérique sera proche de celle du signal analogique.
3. En 24 bits : 224 = 16 777 216 possibilités et en 4 bits : 24 = 16 possibilités
4. Avec 16 possibilités, on ne pourra pas distinguer deux sons d’intensité sonore très proche.
C05 - exercices TSTI2D 7