TP : Etude des paramètres cinétiques d`une réaction chimique

Thème 2 : Lois et modèles
Temps et évolution chimique : cinétique et catalyse
TP : Etude des paramètres cinétiques d’une réaction chimique
Problème : quels paramètres modifient la durée d’une transformation chimique ?
Information : La vitesse de réaction est proportionnelle au nombre de rencontres entre les molécules.
Hypothèses : Formuler des hypothèses pour répondre au problème posé.
Vérification des hypothèses : expérimentation
L’ion thiosulfate S2O32- se transforme progressivement en milieu acide selon la réaction
d’oxydoréduction d’équation :
)(2)()(2
)(
3
2
32 32 lsaq
aq
(aq) OHSSOOHOS  
La formation de particules de soufre solide en suspension opacifie le milieu réactionnel initialement
limpide.
On dispose du matériel suivant :
- Solution S1 de thiosulfate de sodium ( 2Na+(aq) + S2O32-(aq) ) de concentration C1 = 0,2 mol.L-1
- Solution S2 d’acide chlorhydrique ( H3O+(aq) + Cl-(aq) ) de concentration C2 = 0,1 mol.L-1
- Verrerie usuelle
- Plaque chauffante
- Glace
- Chronomètre
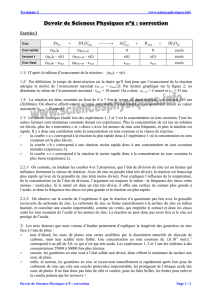
Protocole : pour chaque expérience du tableau ci-dessous
 Introduire dans un bécher (toujours de même taille) placé sur une croix dessinée sur un papier
blanc :
- Ve mL d’eau ;
- V1 mL de la solution de thiosulafate de sodium ;
- V2 mL de la solution d’acide chlorhydrique.
 Déclencher le chronomètre au moment où on ajoute l’acide chlorhydrique
 Se placer au dessus du bécher et mesurer la durée Δt nécessaire à la disparition de la croix.
Expérience
Ve
V1
V2
Température
1
10
20
20
ambiante
2
0
30
20
ambiante
3
0
20
30
ambiante
4
10
20
20
< 10°C (solutions placées dans un bain de glace avant déclenchement)
5
10
20
20
> 40°C (solutions placées dans l’eau chaude avant déclenchement)

Résultats :
Expérience
Paramètre
changeant
Concentrations effectives
Température
(°C)
Δt
[S2O32-] *
[H3O+] *
1
2
3
4
5
* Calcul des concentrations effectives en ion thiosulfate et oxonium à t = 0 :
Conclusions :

TP : Suivi cinétique – τemps de demi-réaction
Lorsqu’un système chimique est en cours de transformation, les quantités des réactifs diminuent tandis
que celles des produits augmentent. On définit l’avancement de la réaction x qui augmente au cours de
la transformation. La réaction évolue jusqu’à atteindre un avancement maximal xmax : on dit que l’état
final est alors atteint.
Pour décrire la durée d’une transformation on utilise souvent le
temps de demi-réaction t1/2 : il s’agit de la durée au bout de
laquelle l’avancement x est égal à la moitié de l’avancement
maximal xmax.
On peut traduire mathématiquement cette définition par :
2
max
2/1 x
tx 
On étudie la réaction entre l’eau oxygénée H2O2 et les ions Iodures I-.
)(2
)(
2
)(
)(
22
)( 222 l
aq
aq
aq
aq OHIHOHI  
Au cours de cette réaction, il se forme du diiode I2, espèce qui colore la solution en jaune-orangé.
On peut donc mesurer l’absorbance de cette solution, due à la formation de diiode.
Document 1 : Spectre d’absorption du diiode :
Document 2 : Tableau d’avancement de la réaction :
)(2
)(
2
)(
)(
22
)( 222 l
aq
aq
aq
aq OHIHOHI  
x = 0
n1
n2
excès
0
x
n1 –2x
n2 – x
excès
x
xmax
n1 – 2xmax
n2 – xmax
excès
xmax
Document 3 : Loi de Beer-Lambert : A = ε . L . [I2]
I. Protocole :
 Choisir la longueur d’onde la mieux adaptée à la mesure de A et étalonner le colorimètre.
 Paramétrage de Latispro : 200 points pendant 15min.
 Dans un bécher de 100mL, on mélange
- V1=20,0mL d’une solution d’iodure de potassium de concentration C1=1,0.10-2mol.L-1.
- 10,0mL d’acide sulfurique à 1 mol.L-1
- 40,0mL d’eau distillée
 A l’instant t=0s (on déclenche le chrono), on ajoute V2=4,0mL d’eau oxygénée de concentration
C2=1,0 mol .L-1 (3,4% en masse de peroxyde d’hydrogène).

 On homogénéise le mélange et on verse rapidement une partie du mélange dans cuve.
 Introduire la cuve dans le colorimètre et déclencher l’acquisition des mesures d’absorbance.
(On supposera que la réaction est suffisamment pour négliger le laps de temps qui s’écoule entre le
départ de la réaction et le début des mesures.)
II. Exploitation :
1. Suivre l’évolution de l’absorbance de la solution en fonction du temps permet de connaître
l’évolution de l’avancement x de la réaction : en répondant aux questions qui suivent, on cherche
à établir une relation entre x et A.
1.1. Calculer n1 et n2. Déterminer le réactif limitant. Calculer xmax.
1.2. Exprimer la concentration de diiode à un instant t en fonction de l’avancement x de la réaction et
du volume de la solution.
1.3. A partir de la loi de Beer-Lambert, montrer que
max
max
x
AA
x
2. A partir de la courbe obtenue, déterminer Amax.
3. En utilisant les fonctionnalités du logiciel, faire calculer x
4. Afficher x en fonction de t.
5. Déterminer t1/2 à l’écran de l’ordinateur. Faire apparaître t1/2 sur la courbe imprimée
6. La méthode utilisée permet-elle de déterminer le temps de demi-réaction de n’importe quelle
réaction ? Justifier.
7. Au bout de combien de fois t1/2 peut-on considérer que la réaction étudiée est terminée ?
8. Faire calculer les quantités n(I-), n(H2O2) et n(I2). Faire apparaître leur évolution sur la courbe.
Imprimer la courbe.

Correction du TP :
1.1. n1 = C1.V1 A.N. n1 = 10-2 × 20×10-3 = 2,0×10-4 mol
n2 = C2. V2 A.N. n2 = 4×10-3 × 1 = 4×10-3 mol
Détermination de xmax :
)(2
)(
2
)(
)(
22
)( 222 l
aq
aq
aq
aq OHIHOHI  
x = 0
n1
n2
excès
0
x
n1 –2x
n2 – x
excès
x
xmax
n1 – 2xmax
n2 – xmax
excès
xmax
Hypothèse :
- Si I- est le réactif limitant : n1 – 2xmax = 0 xmax = n1 / 2 = C1.V1 /2
A.N. xmax = 10-2 × 20×10-3 / 2 = 10-4 mol
- Si H2O2 est le réactif limitant : n2 – xmax = 0 xmax = n2 = C2. V2
A.N. xmax = 4×10-3 × 1 = 4×10-3 mol
L’ion I- est le réactif limitant et xmax = 10-4 mol.
1.2. D’après le tableau d’avancement :
sol
Vx
I
2
1.3. A partir de la loi de Beer-Lambert, on a :
2
IkA 
D’où
k
VA
xSol
Lorsque la réaction est terminée :
kVA
xSol max
max
soit
max
max
A
x
k
VSol 
On peut donc établir l’expression :
max
max
x
AA
x
Résultats :