Correction du TD Physique - Dipôles électrocinétiques et réseaux

Correction du TD Physique - Dipôles électrocinétiques et réseaux en régime permanent - MPSI 1 Lycée Chaptal - 2011
Correction du TD Physique - Dipôles électrocinétiques et réseaux en
régime permanent
I - Équivalences de générateurs
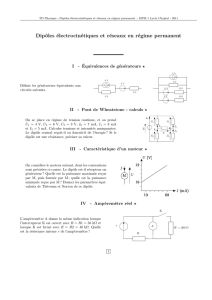
II - Pont de Wheatstone - calculs
La loi des mailles donnent E= 10 V et U4= 7 V soit U= 1 V. La loi des noeuds donne I3= 4 mA,I= 2 mA
et I4= 2 mA. Ainsi défini, le dipôle central est en convention récepteur, de plus l’intensité qui le traverse et la
tension à ses bornes sont positives, c’est donc un récepteur et il reçoit de l’énergie. Si c’était une résistance, sa
valeur serait alors de U/I soit 500Ω.
1

Correction du TD Physique - Dipôles électrocinétiques et réseaux en régime permanent
III - Caractéristique d’un moteur
Le dipôle est en convention récepteur, et la caractéristique montre que tension et intensité associées sont
positives : c’est donc un récepteur. La puissance P=UI est donc reçue, la plus grande possible étant celle obtenue
au « bout de la droite » : Pmax = 720 mW, et la plus petite Pmin = 0 mW - qui sont aussi, de fait, respectivement
les plus petites et grandes fournies (au signe près) ! Ce dipôle est un récepteur actif puisque sa caractéristique ne
passe pas par l’origine. Le générateur de Thévenin équivalent a pour loi U=ETh +RThI, que l’on obtient en
regardant l’ordonnée à l’origine (et ainsi ETh = 10 V) et la pente (ce qui donne RTh = 33Ω). En Norton, on a
alors RTh = 33Ω et INo = 300 mA).
IV - Ampèremètre réel
Lorsque K est ouvert, on a un circuit série avec e, la réstistance Ret l’ampèremètre, parcouru par un courant
i0=e/(r+R1). Lorsque K est fermé, on a, d’après le schéma,
e=ri1+R2iet ri1=R0(i−i1)
soit i1=e
r+R2(R0+r)/R0
Si l’indication est la même sur l’ampèremètre, c’est que les deux intensités sont les mêmes, soit i0=i1et
e
r+R1
=e
r+R2(R0+r)/R0
conduisant à r=R0R1
R2−1= 50Ω
2

Correction du TD Physique - Dipôles électrocinétiques et réseaux en régime permanent - MPSI 1 Lycée Chaptal - 2011
V - Adaptation en puissance
BConnaître cet exercice est importantissime ! !
D’après le circuit, on a i=E/(R+r), et on a aux bornes de la
résistance par pont diviseur
U=R
R+rE
soit une puissance P=Ui =RE2
(R+r)2
Si on dérive cette puissance par rapport à R, on a
∂P
∂R =E2 (R+r)21−2R R+r
qui est nul pour R=R0=ret on a alors
P=Pmax =E2
4r
Remarquons que le générateur fournit de son côté Pgéné =Ei =E2
2r. Le rendement vaut donc η=Pmax Pgéné
= 50%.
On dit que choisir R=rcorrespond à effectuer l’adaptation en puissance.
VI - Composant non linéaire
On a [I] = [a]×[U]3,as’exprime donc en A.V −3.
On peut écrire grâce à la loi des mailles (une seule maille, donc un seul courant I) que
e=RI +U, avec I=gU +aU3
soit e= (Rg + 1) U+Ra U3
Numériquement, 4 = 3 U+U3
soit U= 1 V et I= 3 mA
On a alors successivement
Pgéné =eI = 12 mW PR=RI2= 9 mW Pdipôle =UI = 3 mW
Ainsi, on remarque que Pgéné =PR+Pdipôle : on a conservation de la puissance, celle-ci, fournie par le générateur,
se répartit entre le dipôle et la résistance.
3

Correction du TD Physique - Dipôles électrocinétiques et réseaux en régime permanent
VII - Étude d’un voltamètre ou électrolyseur
Pour ce voltamètre, il faut faire plusieurs hypothèses. Supposons tout d’abord i > 0, on a alors le schéma
équivalent suivant (le voltamètre se comportant comme un générateur en opposition). Notons que dans ce cas
10|i|= 10i.
On a E= 150 + 100i+ 10i2par la loi des mailles. Cette in-
tensité n’existe que si le discriminant ∆est positif ou nul, ie si
E>−100 V . Dans ce cas, l’intensité vaut −5 + √∆/2, l’autre
solution conduisant à une solution négative. Pour avoir une in-
tensité positive (notre hypothèse), il faut donc que ∆>100, soit
E>150 V ce qui est cohérent avec E>−100 V.
Dans un second temps, supposons i < 0, dans ce cas 10|i|− = 10i
et on a le nouveau schéma ci-contre. Cette fois-ci E=−50+100i−
10i2. Cette intensité n’existe que si le discriminant ∆0est positif
ou nul, ie si E6200 V . Dans ce cas, l’intensité vaut 5−√∆0/2,
l’autre solution conduisant à une solution positive. Pour avoir une
intensité négative (notre hypothèse), il faut donc que ∆0>100,
soit E6−50 V ce qui est cohérent avec E6200 V.
Remarquons qu’alors, les deux allures de i=f(E)sont celles de
deux paraboles. Enfin, pour toute autre valeur de E, on n’a ni
i > 0ni i < 0:iest donc nulle. D’où l’allure finale :
VIII - Transformations de Kennelly
On suit scrupuleusement les indications de l’énoncé. Tout d’abord, on a de façon évidente
ia+ib+ic= 0 et Uab +Uca +Ubc = 0
Par ailleurs, on peut écrire
Uab =aia−bib
puis ia=Uab
C−Uca Bet ib=Ubc A−Uab C
En combinant ces deux expressions, Uab =a
CUab −a BUca −b AUbc +b CUab
soit Uab 1−a+b
C=−a BUca +b AUbc
Or, on sait que Uab =−Uca +Ubc
Par identification, puisque cette égalité doit être vraie pour toute tension, on a
4

Correction du TD Physique - Dipôles électrocinétiques et réseaux en régime permanent - MPSI 1 Lycée Chaptal - 2011
a
B= 1 −a+b C=b A
ce qui conduit à 1−a+b
C= 1 −a C−b C= 1 −a C−A BC a=a B
et enfin 1 = a1
B+1 C+A BC =aA+B+C BC 
qui est le résultat annoncé. On conclut de même par permutation circulaire pour les deux autres identités. En
combinant ces expressions, ou en tenant un raisonnement similaire sur les conductances, on peut également obtenir
le résultat donnant A,Bet Cen fonction uniquement de a,bet c.
BSi on utilise ce résultat, il faut être capable de le redémontrer, car il n’est pas au programme. Ainsi,
à l’écrit, ne pas l’utiliser (ou alors, refaites toute la démonstration auparavant ...), et à l’oral, vous pouvez vous
permettre de l’utiliser, et de ne le démontrer que si on vous en fait la demande. Mais dans ce dernier cas, il vaut
mieux pour vous que vous ne vous trompiez pas !
IX - Résistance itérative
Dans ce premier cas, on a le schéma ci-contre. Attention, les trois résistances
extérieures sont en série, et la résistance équivalente est en parallèle avec la
dernière ! La résistance équivalente totale vaut donc
R1=3
4r
Second cas, même principe, et on utilise le résultat
précédent. La résistance équivalente totale vaut
R2=11
15 r
Pour le dernier cas, considérons la cellule de taille net relions-la à la résistance équivalente de taille n−1grâce au
schéma ci-dessous.
On obtient la relation de récurrence 1
Rn
=1
r+1 2r+Rn−1
soit Rn=2r+Rn−1
3r+Rn−1
r=r−r2
3r+Rn−1
C’est une suite du type un+1 =f(un)avec fcroissante et majorée par 1. Elle est donc convergente, et tend vers
une limite R∞, vérifiant
5