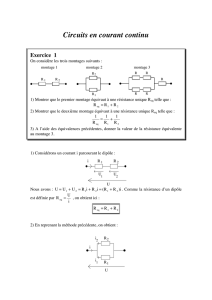
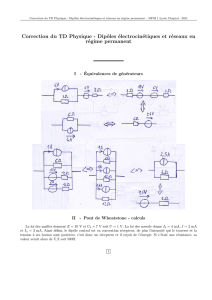
Loi des noeuds - loi des mailles

R1R2R3
U2 U1U3
UAB
A B
I
1et_ch2(Les dipôles passifs).odt - Marie Pierrot – Lycée du Rempart - 22/09/09
Ch.2 : LES DIPOLES PASSIFS
Def: Un dipôle passif est un dipôle récepteur (sa caractéristique passe par l'origine). Il reçoit de l'énergie électrique qu'il
perd sous forme de chaleur (effet Joule).
1. Classification des dipoles passifs.
Classification
DIPOLES PASSIFS
linéaires non linéaires
symétriques asymétriques
Nom
Résistance Thermistance (C.T.N.) Varistance Diode Diode Zener
SymboleCaractéristiqueRemarques
La caractéristique est
une droite dont
l’équation s’écrit
simplement:
U = RI ou I = GU
La résistance du dipôle
varie avec la
température.
Résistance dont la
valeur dépend de la
tension appliquée.
Composant qui laisse
passer le courant dans
un seul sens: le sens
direct.
Diode particulière qui
ne laisse passer le
courant « en inverse »
qu’à partir d’un seuil de
tension inverse.
Commentaire: Il existe d’autres type de dipôles résistifs: les magnétorésistances(...), les photorésistances(...),. et d’autres types de diodes: les
photodiodes...
2. Association de resistances
2.1. Association en série.
Des dipôles sont associés en série s'ils sont traversés par le même courant.
Problème posé:
Trouver une résistance unique, équivalente, qui, soumise à la même tension U serait parcourue par un courant de même
intensité I.
est équivalent à :
Loi d’additivité des tensions: UAB = U1 + U2 + U3 (1)
Loi d’Ohm: U1 = R1 I ; U2 = R2 I ; U3 = R3 I et UAB = Req I (2)
(1) + (2)  Req I = R1 I + R2 I + R3 I
 Req I = ( R1 + R2 + R3 ) × I soit Req = R1 + R2 + R3
Page 1 sur 3
RE Q
UA B
A B
I
I
U
I
U
I
U
I (A)
U (V)
I (A)
U (V)
I (A)
U (V)
T1
T2
I (A)
U (V)
I (A)
U (V)
U
I
U
T
I
U

1et_ch2(Les dipôles passifs).odt - Marie Pierrot – Lycée du Rempart - 22/09/09
Conclusion: Si le dipôle est constitué de n résistances en série, alors la résistance équivalente à ce dipôle est la somme
de toutes les résistances.
Rmq: - Si toutes les résistances sont identiques et égales à R alors Req = n × R
- En série, la résistance équivalente est supérieure ou égale à la plus grande des résistances associées.
- L'association en série augmente la résistance équivalente.
2.2. Association dérivation :
Des dipôles sont associés en dérivation s'ils ont la même différence de potentiel à leurs
bornes, donc si leurs bornes sont communes.
On se pose le même problème que pour l’association en série :
est équivalent à
Loi des noeuds: I = I1 + I2 + I3 (1)
Loi d’Ohm: I1 = G1 U ; I2 = G2 U ; I3 = G3 U et I = Geq U (2)
(1) + (2)  Geq U = G1 U + G2 U + G3 U
 Geq U = ( G1 + G2 + G3 ).U soit Geq = G1 + G2 + G3
Si le dipôle est constitué de n résistances en dérivation, alors la conductance équivalente à ce dipôle est la somme des
de toutes les conductances.
Rmq: - Si n = 2 :
1 2
eq
1 2
R .R
R =R +R
- Si toutes les résistances sont identiques et égales à R alors
- En dérivation, la résistance équivalente est inférieure ou égale à la plus petite des résistances associées.
- L'association en dérivation diminue la résistance équivalente.
Exercice d'application II-1
Dans le cas de l’association en série de trois résistances: R1 = 4 k ; R2 = 6 k ; R3 = 12 k :
1) Calculer la résistance équivalente.
2) Calculer l’intensité du courant commun aux trois résistances sachant que la tension aux bornes de l'ensemble est :
U = 11 V.
3) Calculer la tension aux bornes de chacune des trois résistances.
Exercice d'application II-2
Dans le cas de l’association en parallèle de trois résistances: R1 = 4 k ; R2 = 6 k ; R3 = 12 k :
1) Calculer la conductance équivalente et en déduire la résistance équivalente.
2) Calculer la tension commune appliquée aux trois résistances sachant que l'intensité du courant traversant le
groupement est I = 0,5 mA..
3) Calculer l’intensité du courant traversant chacune des trois résistances.
Page 2 sur 3
Req = R1 + R2 + ... + Rn
Geq = G1 + G2 + ... + Gnou
R1
R2
R3
I1
I2
I3
I
UA B
A B
RE Q
UA B
A B
I
eq
R
R = n
= + + +
EQ 1 2 n
1 1 1 1
...
R R R R

E
R1
R2U
M
A
1et_ch2(Les dipôles passifs).odt - Marie Pierrot – Lycée du Rempart - 22/09/09
3. Diviseurs de tension et de courant
3.1. Diviseur de tension.
La structure est conforme au schéma ci-contre :
Exercice d'application III-1.
1) Exprimer U en fonction de I et R2.
2) Exprimer I en fonction de E, R1 et R2.
3) Exprimer U en fonction de E, R1 et R2.
Réponse :
U=R2
R1R2
×E
Rmq: - R1 + R2 > R2  U < E d’où le nom de cette structure.
- De nombreuses structures peuvent être équivalente à celle-ci par association de résistances, cette formule est donc applicable
dès qu’il est possible d’identifier R1 et R2.
3.2. Diviseur de courant
La structure est la suivante :
Exercice d'application III-2.
1) Exprimer I en fonction de U et R2.
2) Exprimer U en fonction de Icc, R1 et R2, puis en fonction de Icc, G1 et G2.
3) Exprimer I en fonction de Icc, G1 et G2.
Réponse :
I=G2
G1G2
×ICC
Rmqs: - G1 + G2 > G2  I < Icc d’où le nom de cette structure.
- De la même façon que le diviseur de tension, cette formule est utilisable dans de nombreux cas.
Exercices III-3 (quelques gammes…)
Page 3 sur 3
R2U
M
A
R1
Icc
E
R
R
R
U=f(E)? E
R
2R
3R
U=f(E)?
100 Ω
12 V 330 Ω
50 Ω
U?
R RαU=f(E)?
E
E
R
R
R
R
R R
U=f(E)?
R1
R2
R3
R4
E
U1 ?
U2 ?