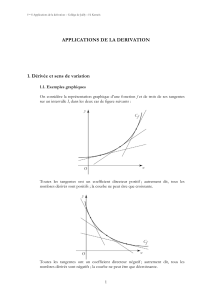
2007

22 2008 2
4
5+2
f: [a, b]→[a, b] (un)
un+1 =f(un)
u0∈[a, b]
(un)
f u0< f(u0) (un)
α f(x) = x
f u0> f(u0)
un+1 =√3 + un
u0= 1
f f ◦f
(u2n) (u2n+1)
7
f:R→Rf(x)=(x2+ 1) arctan(x)
f
f±∞
f0 3 0
g=f−1
g(0)
g g0(0)
0Cgg
g00 g000 g00 (0) = 0 g000 (0) 60
CfCg
0
g=f−10 3
g(x) = a0+a1x+a2x2+a3x3+x3(x)
a0= 0
0 3 f◦g a1, a2, a3
f(g(x)) = x a1a2a3
11 2007

22 2008 2
9
f
I f0
I
f:
[−1; 1] →R
x7→ x2sin( 1
x)x6= 0
0x= 0
f[−1; 1] f0(0)
h:
[−1; 1] →R
x7→ 2xsin( 1
x)−cos( 1 x)x6= 0
0x= 0
f I ⊂Ra < b
I f0(a)< f0(b)y f0(a)< y < f0(b)
g[a, b]g(x) = f(x)−xy
g0
g
[a, b]
g0(a)<0g0(b)>0
g a
limx→ag(x)−g(a)
x−a
g b
c∈]a, b[f0(c) = y
f0
f0(a)< f0(b)
f0
[a, b]f0(a)> f0(b)
h
11 2007

22 2008 2
7
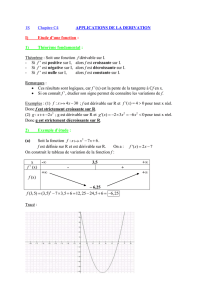
u0∈[a, b]a6u06b n >1un=f(un−1)∈[a, b]f([a, b]) ⊂[a, b]
n∈Na6un6b
f u0< f(u0) (un)
n= 0 u0< f(u0) = u10
n un6un+1 f(un)6f(un+1)f
un+1 6un+2 n+ 1
(un) (un)
α(un)f
α= limn→+∞un+1 = limn→+∞f(un) = f(α)
u0> f(u0)
0u0> f(u0) = u1
n un>un+1 f(un)>f(un+1)f
un+1 >un+2 n+ 1
un+1 =√3 + u
u0= 1
f: [0,3] →[0,3] [0,3]
f(x) = √3 + x√f u1=
f(u0) = f(1) = √4 = 2 > u0(un)
α α =√3 + α α α2= 3 + α
α2−α−3=0 α1=1−√13
2α2=1 + √13 2α1<1 = u0
(un)α=1 + √13
2
f∀x, y ∈[a, b]x6y
x6y⇒f(x)>f(y)⇒f(f(x)) 6f(f(y))
f◦f un=f(un−1) = f(f(un−2))
u2n=f◦f(u2(n−1))
u0∈[a, b]u2n+1 =f◦f(u2n−1) u1∈[a, b]
f◦f
u0−u2(u2n)u1−u3(u2n+1)
7
f0(x) = 2xarctan(x) + 1 [0,+∞[x>0 arctan(x)>0 2xarctan(x)>0
f0(x)>1 [0,+∞[ ] − ∞,0] x60 arctan(x)60
2xarctan(x)>0f0(x)>1 ] − ∞; 0] f
Rf(R)
f(R) = R
11 2007

22 2008 2
flimx→−∞ f(x) = −∞ limx→+∞f(x)=+∞
3 0 arctan arctan(x) = x−x3
3+x3(x) limx→0(x)=0
f(x)=(x2+ 1)(x−x3
3) + x31(x) = x+2 3x3+x32(x) 0
f(0) = 0 g(0) = g(f(0)) = f−1(f(0)) = 0
f0f0(x)>1x∈R
R
g0(0) = 1
f0(f−1(0)) =1 f0(0) = 1
1 (0,0)
y=x
f0 0 f
f g (0,0)
y=x0
g g00 (0) = 0
f0f000 (0) >0
g000 (0) >0g000 (0) 60
a0=g(0) = 0
g(x) = a1x+a2x2+a3x3+x31(x)
f(x) = x+2
3x3+x32(x)
f◦g(x)=(a1x+a2x2+a3x3) + 2
3(a1x+a2x2+a3x3)3+x33(x)
=a1x+a2x2+ (a3+2
3a3
1)x3+x34(x)
f◦g(x) = x
a1x+a2x2+ (a3+2
3a3
1)x3+x34(x) = x
a1= 1 a2= 0 a3=−2
3a3
1=−2
3
9
fR∗0−16sin( 1
x)61⇒ −x26
f(x)6x2limx→0f(x) = f(0) = 0
x f f0(x) =
2xsin( 1
x)−cos( 1 x)f0
lim
x→0
f(x)−f(0)
x= lim
x→0xsin( 1
x)=0
f0(0) = 0
R
x→2xsin( 1
x) 0 x→0x→cos( 1 x)
x→0h0
g g0(x) = f0(x)−y
11 2007

22 2008 2
g[a, b]
c∈[a, b]g(c)g[a, b]
g0(a) = f0(a)−y < 0y > f0(a)g0(b) = f0(b)−y > 0
y < f0(b)
g a
x∈[a, b]g(x)−g(a)>0g(x)−g(a)
x−a>0x→a
g0(a)>0
g[a, b]b x ∈[a, b]
g(x)6g(b)g(x)−g(b)
x−b60x→b
g0(b)60g
a b
c∈]a, b[
g0(c) = 0 f0(c)−y= 0
c∈]a, b[f0(c) = y f0
[a, b]
f0(a)> f0(b)y f0(a)> y > f0(b)
g g(x) = f(x)−xy
g0(a)>0g0(b)<0c∈[a, b]g(c)
g[a, b]g
a b c ∈]a, b[f0(c) = y g0(c)=0
f0[a, b]
h=f0
h
11 2007