Chapitre 8. Intégration

Chapitre 8. Intégration
(rappels et compléments)
I. Découverte de la notion d’intégrale
On sait calculer l’aire d’un rectangle :
L
ℓaire=L×ℓ
l’aire d’un triangle
b
haire=base ×hauteur
2=b×h
2
l’aire d’un trapèze rectangle
B
b
haire=(petite base +grande base)
2×hauteur
=(b+B)
2×h
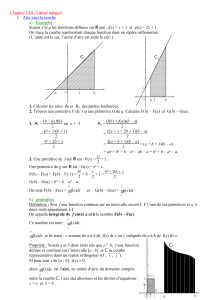
Le plan étant rapporté à un repère orthonormé O, →
i , →
j, on se propose de calculer l’aire du domaine Ddu plan
compris entre l’axe des abscisses, les droites d’équation x=0et x=1et la courbe représentative de la fonction
xx2. Ainsi, on cherche à déterminer l’aire d’un domaine où au moins un des bords « est courbe ».
1
1
aire=?
L’unité dans laquelle sera mesurée cette aire est l’unité d’aire, c’est-à-dire l’aire du carré de sommets de
coordonnées (0,0),(1,0),(1,1)et (0,1). L’aire Ade Dest certainement inférieure à une unité d’aire
© Jean-Louis Rouget, 2015. Tous droits réservés. 1 http ://www.maths-france.fr

1
1
ou même à une demie unité d’aire
1
1
et est par exemple supérieure à 0,5×0,25 =0,125.
1
1
0,5
0,25
Ainsi, 0,125 ⩽A⩽0,5. On veut faire bien mieux que cela. On veut la valeur exacte de A. On peut améliorer les
idées précédentes dont le but est d’encadrer A. On note A1la somme des aires des rectangles ci-dessous.
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
0,01
0,04
0,09
0,16
0,25
0,36
0,49
0,64
0,81
1
1
y=x2
© Jean-Louis Rouget, 2015. Tous droits réservés. 2 http ://www.maths-france.fr

On a
A⩾A1
=0,1×0+0,1×0,01 +0,1×0,04 +0,1×0,09 +0,1×0,16 +0,1×0,25 +0,1×0,36 +0,1×0,49
+0,1×0,64 +0,1×0,81
=0,1(0+0,01 +0,04 +0,09 +0,16 +0,25 +0,36 +0,49 +0,64 +0,81)
=0,1×2,49 =0,249.
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
0,01
0,04
0,09
0,16
0,25
0,36
0,49
0,64
0,81
1
1
En notant A2la somme des aires des rectangles ci-dessus, on a aussi
A⩽A2
=0,1×0,01 +0,1×0,04 +0,1×0,09 +0,1×0,16 +0,1×0,25 +0,1×0,36 +0,1×0,49 +0,1×0,64
+0,1×0,81 +0.1×1
=A1−0,1×0+0.1×1=A1+0,1
=0,349.
On a ainsi obtenu 0,249 ⩽A⩽0,349. Il faut encore améliorer en donnant aux rectangles ci-dessus des largeurs
aussi petites que l’on veut. On découpe l’intervalle [0,1]non plus en 10 parties égales mais en nparties égales où
nest un entier naturel non nul que l’on fera ensuite tendre vers +∞.
L’intervalle [0,1]est découpé en les nintervalles 0,1
n,1
n,2
n,2
n,3
n,3
n,4
n,...,n−3
n,n−2
n,n−2
n,n−1
n,
n−1
n,n
n=1−1
n,1. De manière générale, l’intervalle [0,1]a été décomposé en la réunion des nintervalles
de la forme k
n,k+1
noù kest un entier naturel tel que 0⩽k⩽n−1.
© Jean-Louis Rouget, 2015. Tous droits réservés. 3 http ://www.maths-france.fr

1
n
2
n
3
n
k
n
k+1
n
n−1
n1
(k/n)2
((k+1)/n)2
Chaque intervalle k
n,k+1
na une longueur égale à la différence k+1
n−k
n=1
n. Quand nous ferons tendre n
vers +∞, la longueur de l’« intervalle » obtenu sera notée dx (différence infinitésimale de valeurs de la variable x).
Sur l’intervalle k
n,k+1
n, l’aire sous la courbe représentative de la fonction xx2est comprise entre l’aire du
petit rectangle 1
n×fk
n=1
n×k
n2
et l’aire du grand rectangle 1
n×fk+1
n=1
n×k+1
n2
. Ainsi,
• sur l’intervalle 0,1
n, l’aire sous le graphe de la fonction xx2est comprise entre 1
n×f(0)et 1
n×f1
n,
• sur l’intervalle 1
n,2
n, l’aire sous le graphe de la fonction xx2est comprise entre 1
n×f1
net 1
n×f2
n,
• sur l’intervalle 2
n,3
n, l’aire sous le graphe de la fonction xx2est comprise entre 1
n×f2
net 1
n×f3
n,
⋮
• sur l’intervalle n−1
n,n
n, l’aire sous le graphe de la fonction xx2est comprise entre 1
n×fn−1
n
et 1
n×fn
n.
En additionnant toutes ces inégalités, on obtient
A⩾1
nf(0)+f1
n+f2
n+...+fn−3
n+fn−2
n+fn−1
n
et
A⩽1
nf1
n+f2
n+f3
n+...+fn−2
n+fn−1
n+f(1).
Les deux sommes ont beaucoup de termes en commun et donc la différence entre le majorant fourni et le minorant
fourni est très simple. Elle est égale à
1
n(f(1)−f(0))=1
n(1−0)=1
n.
Quand ntend vers +∞, on est en droit d’espérer que le minorant fourni et le majorant fourni aient une limite
commune (ce que l’on va effectivement démontrer plus loin). Cette limite commune sera par définition l’aire A.
Cette aire sera ainsi obtenue comme une somme infinie d’aires de rectangles de largeurs infinitésimales dx
(différence de valeurs de x) et de longueurs f(x) où xest un réel variant de 0 à 1. On a la notera
A=∫1
0
f(x)×dx =∫1
0
x2×dx =∫1
0
x2dx,
© Jean-Louis Rouget, 2015. Tous droits réservés. 4 http ://www.maths-france.fr

(le symbole ∫est donc la lettre s en majuscule, s étant l’initiale du mot somme).
Il nous reste à étudier la limite de chacun des deux membres de l’encadrement de Afourni plus haut.
Pour tout entier naturel non nul, on pose un=12+22+32+...+(n−2)2+(n−1)2+n2
ntermes
.
Ainsi, u1=12=1,u2=12+22=5,u3=12+22+32=14,u4=12+22+32+42=30 ...
L’encadrement de Aobtenu plus haut s’écrit maintenant pour tout entier naturel non nul n,
1
n×02+12+22...+(n−1)2
n2⩽A⩽1
n×12+22...+(n−1)2+n2
n2.
ou encore
un
n3−1
n⩽A⩽1
n×un
n3,(I)
(nous avons constaté plus haut que le premier membre de l’encadrement était 1
nau-dessous du second membre).
Nous allons maintenant donner unen fonction de n. Nous nous contenterons de démontrer une formule par
récurrence sans expliquer comment nous avons deviné cette formule ou plutôt sans expliquer le calcul direct qui
nous a permis de la découvrir.
Montrons par récurrence que pour tout entier naturel non nul n,un=n(n+1)(2n+1)
6.
•u1=12=1et 1×(1+1)×(2×1+1)
6=2×3
6=1. Donc u1=1×(1+1)×(2×1+1)
6et la formule
à démontrer est vraie quand n=1.
• Soit n⩾1. Supposons que un=n(n+1)(2n+1)
6et montrons que un+1=(n+1)((n+1)+1)(2(n+1)+1)
6.
un+1=12+22+32+...+(n−1)2+n2+(n+1)2=un+(n+1)2
=n(n+1)(2n+1)
6+(n+1)2(par hypothèse de récurrence)
=(n+1)n(2n+1)
6+(n+1)=(n+1)×n(2n+1)+6(n+1)
6=(n+1)×2n2+n+6n+6
6
=(n+1)×2n2+7n+6
6=(n+1)×(n+2)(2n+3)
6=(n+1)((n+1)+1)(2(n+1)+1)
6.
On a montré par récurrence que pour tout entier naturel non nul n,un=n(n+1)(2n+1)
6.
On peut maintenant déterminer la valeur exacte de Apar passage à la limite quand ntend vers +∞.
Pour tout entier naturel non nul n,
un
n3=n(n+1)(2n+1)
6n3=(n+1)(2n+1)
6n2=2n2+3n+1
6n2=2n2
6n2+3n
6n2+1
6n2
=1
3+1
2n+1
6n2.
L’encadrement (I)s’écrit alors pour tout entier naturel non nul n:
1
3+1
2n+1
6n2−1
n⩽A⩽1
3+1
2n+1
6n2.
Quand ntend vers +∞, le membre de gauche et le membre de droite de l’encadrement ci-dessus tendent tous deux
vers 1
3. Quand ntend vers +∞, on obtient 1
3⩽A⩽1
3et on a donc montré que
A=∫1
0
x2×dx =1
3.
© Jean-Louis Rouget, 2015. Tous droits réservés. 5 http ://www.maths-france.fr
 6
6
 7
7
 8
8
 9
9
 10
10
 11
11
 12
12
 13
13
 14
14
 15
15
 16
16
 17
17
 18
18
 19
19
 20
20
 21
21
 22
22
 23
23
 24
24
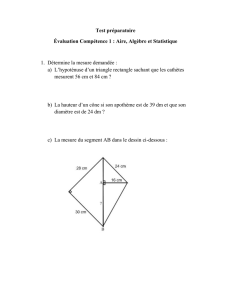
1
/
24
100%