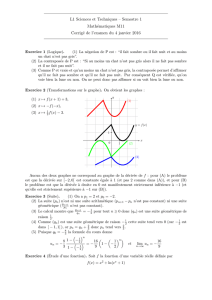
Trigonométrie hyperbolique. On définit trois fonctions

Case 2D5000, 292 rue Saint-Martin 75141 Paris Cedex 03
Bureau 17.0.14
Tel: [phone], Mel: thierry[email protected]
Conservatoire National des Arts et Métiers
Département d’Ingénierie Mathématique
MVA006 - Mathématiques
2012–2013 T. Horsin
Trigonométrie hyperbolique.
On définit trois fonctions
sh :R→R,x7→ ex−e−x
2
ch :R→R,x7→ ex+e−x
2
th :R→R,x7→ sh(x)
ch(x)
Comme ∀x∈R,ex>0alors ch(x)>0donc ces trois fonctions sont définies sur R.
On vérifie que (sh)0=ch, (ch)0=sh, (th)0= 1 −th2=1
ch2.
La fonction ch étant >0, sh est une fonction strictement croissante, et comme sh(0) =
1−1
2= 0, sh est négative sur R−et est positive sur +∞.
sh est impaire comme th tandis que ch est paire.
On a lim
+∞sh(x) = lim +∞ch(x) = +∞tandis que dim lim+∞th(x) = 1.
y=ch(x)
y=sh(x)
y=th(x)
Figure 1

Case 2D5000, 292 rue Saint-Martin 75141 Paris Cedex 03
Bureau 17.0.14
Tel: [phone], Mel: thierry[email protected]
Conservatoire National des Arts et Métiers
Département d’Ingénierie Mathématique
La fonction ch est strictement croissante sur [0,+∞[et comme ch(0) = 1 et lim
+∞ch(x) =
+∞, ch définit une bijection de [0,+∞[sur [1,+∞[. La fonction réciproque argch est
strictement croissante de [1,+∞[sur [0,+∞[.
On a (argch)0(x) = 1
sh(argch(x)). Or on vérifie facilement que
ch2(x)−sh2(x) = 1,
donc (argch)0(x) = 1
√x2−1.
La fonction sh est strictement croissante sur ]− ∞,+∞[et comme lim
−∞ sh(x) = −∞ et
lim
+∞sh(x)=+∞, sh définit une bijection de ]− ∞,+∞[sur ]− ∞,+∞[. La fonction
réciproque argsh est strictement croissante de ]−inf ty,+∞[sur ]− ∞,+∞[.
On a (argsh)0(x) = 1
ch(argsh(x)). Or on vérifie facilement que
ch2(x)−sh2(x) = 1,
donc (argsh)0(x) = 1
√x2+ 1
.
La fonction th est strictement croissante sur ]− ∞,+∞[et comme lim
−∞ sh(x) = −1
et lim
+∞sh(x) = +1, sh définit une bijection de ]− ∞,+∞[sur ]−1,+1[. La fonction
réciproque argth est strictement croissante de ]−1,+1[ sur ]− ∞,+∞[.
On a (argth)0(x) = 1
1−th2(argth(x)).
Donc (argth)0(x) = 1
1−x2.
Déterminons une expression de argch(x)argsh(x)et argth(x).
Si y=ch(x)alors
ex+e−x= 2ysoit X2+ 1 −2yX = 0 avec X=ex. Cette équation a un discriminant de
4y2−4>0puisque y≥1.
On a X=y±py2−1. Comme x≥0alors X≥1, ce qui donne X=y+py2−1,
donc argch(y) = ln(y+py2−1) .
Si y=sh(x)alors

Case 2D5000, 292 rue Saint-Martin 75141 Paris Cedex 03
Bureau 17.0.14
Tel: [phone], Mel: thierry[email protected]
Conservatoire National des Arts et Métiers
Département d’Ingénierie Mathématique
ex−e−x= 2ysoit X2−1−2yX = 0 avec X=ex. Cette équation a un discriminant de
4y2+ 4 >0
Comme X>0, on a X=y+py2+ 1.
donc argsh(y) = ln(y+py2+ 1) .
Si y=th(x)alors
ex−e−x=y(ex+e−x)soit e2x−1 = y(e2x+ 1) ou encore e2x(1 −y) = 1 + ydonc
e2x=1 + y
1−y, soit x=1 2ln( 1 + y 1−y).
Donc argth(y) = 1
2ln( 1 + y 1−y).
On dipose de formules de trigonométrie.
Par exemple
sh(2x) = e2x−e2x
2= 2ex−e−x 2
ex+e−x
2.
ch(2x) = e2x+e2x
2= 2ch2(x)−1.