planche 13 _ redresseur commande

M. Dedieu ; Lycée J.Perrin (95) 1
http://maphysiqueappliquee.free.fr
Terminale GET
EXERCICES : planche 13
Redresseur commandé
Exercice 1 :
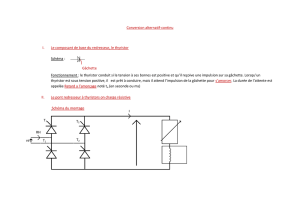
On utilise un pont mixte monophasé pour alimenter un moteur à courant continu que nous
considérerons ici comme étant constitué d'une force électromotrice E en série avec une résistance
interne faible. Le moteur est monté en série avec une bobine parfaite; celui-ci est alors traversé par un
courant parfaitement lissé. La tension u délivrée en entrée du convertisseur par un alternateur a une
valeur efficace U=110 V et une fréquence f = 50 Hz.
Les thyristors et les diodes sont considérés comme parfaits. On appelle θ 1'angle de retard à
l'amorçage des deux thyristors du pont.
1) Pour visualiser simultanément la tension uc et l'intensité ic, on doit ajouter un élément dans le
montage ci-contre. Préciser en justifiant votre réponse, la nature et le montage de cet élément en vous
aidant des listes proposées ci-dessous
a - bobine d'inductance 25 mH, 1 - en série avec l'induit et la bobine,
b - condensateur de capacité 0,3 mF, 2 - en parallèle avec l'induit,
c - résistance de 15 Ω, 3 - en parallèle avec l'induit et la bobine,
d - résistance de 0,10 Ω
2) pour un angle de retard à l'amorçage θ égal à π/ 3 , tracer les variations de u
c
en fonction du
temps.
3) on veut mesurer la valeur efficace de la tension de u c avec un voltmètre. Indiquer les deux
types d'appareils de mesure utilisés et la position dans laquelle on les utilise.
4) La résistance d'induit étant très faible, on la néglige et on écrit que E = < u
c
> où E est la f.e.m.
induite du moteur, et < u
c
> la valeur moyenne de la tension u
c
.
a - donner la formule permettant de calculer cette tension et faire l'application
numérique.
b - Quel est l'avantage d'un pont mixte par rapport à un pont à 4 diodes ?
Pont monophasé mixte alimentant un moteur à courant continu

M. Dedieu ; Lycée J.Perrin (95) 2
http://maphysiqueappliquee.free.fr
Exercice 2 :
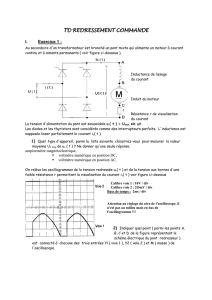
Un pont redresseur à quatre thyristors alimente sous une tension u
MN
un récepteur inductif (moteur à
courant continu) à partir d'un réseau fournissant une tension sinusoïdale v = V√2 sin ωt , V = 220 V de
fréquence f = 50 Hz. On admettra que le récepteur est suffisamment inductif pour que le courant i qui
le traverse soit considéré comme constant : i = I = 10 A.
Les thyristors Th1 et Th3 reçoivent sur leur gâchette des impulsions aux instants : t
0
, t
0
+ T, ...
Les thyristors Th2 et Th4 reçoivent sur leur gâchette des impulsions aux instants : t
0
+ T/2 , to + 3T/2.
Ces thyristors sont supposés parfaits.
1. Dans l'intervalle de temps (t
0
, t
0
+ T), préciser et justifier la durée de conduction de chaque
thyristor (t
0
est compris entre 0 et T/2).
Exprimer u
MN
en fonction de v.
2. Pour t
0
= T/8 , représenter graphiquement : les tensions v et u
MN
, les courants i
1
, i
2
et i
s
.
3. Etablir la relation donnant la valeur moyenne < u
MN
> de la tension u
MN
en fonction de V et t
0
.
Calculer < u
MN
> pour t
0
= T/8
Entre quelles valeurs varie < u
MN
> lorsque t
0
varie de 0 à T /4 ?
4. Pour I = 10 A, t
0
= T/4, calculer la puissance absorbée par le récepteur.

M. Dedieu ; Lycée J.Perrin (95) 3
http://maphysiqueappliquee.free.fr
Exercice 3 :
On étudie le pont mixte suivant. On donne u
2
= 72 sin(ωt) lorsque u
2
est exprimé en volts.
L'inductance L est supposée suffisante pour que le courant soit considéré comme constant : i= I = 2 A.
1. Que faut-il ajouter au schéma précédent pour visualiser la forme du courant i ? Comment brancher
un oscilloscope qui permettra de visualiser simultanément u(t) et i(t).
2. Tracer en concordance de temps avec u
2
, les allures de la tension u(t) et du courant i(t) , sachant que
les thyristors Th
l
et Th
2
sont respectivement commandés aux instants T/8 et 5T/8.
3. Déterminer l'angle d'amorçage α du thyristor Th
l
.
4. Calculer la valeur moyenne de u sachant que : < u >=
U
2max
(1+cos
α
)
π

M. Dedieu ; Lycée J.Perrin (95) 4
http://maphysiqueappliquee.free.fr
Exercice 4 :
Bac 96 Polynésie : Redressement commandé
Afin de régler la tension aux bornes de l'induit du moteur à courant continu à excitation séparée
(étudié dans la partie précédente), on utilise un pont tout thyristors (Figure 1).
Le moteur travaille à excitation constante.
En série avec l'induit du moteur on a placé une bobine. Quel est son rôle ?
On donne sur le document réponse (Figure 3), l'allure de la tension d'alimentation à l'entrée du pont
u
A
(t) et de l'intensité i(t) traversant le moteur. u
A
= U
max
sin ωt avec U
max
= 400 V.
L'angle de retard à l'amorçage est noté δ.
Sur la figure 3 :
préciser, en les hachurant, les intervalles de conduction de chacun des thyristors ;
tracer l'allure de la tension us(t) en sortie du pont redresseur ;
tracer l'allure de l'intensité i
TH1
(t) du courant qui traverse le thyristor TH
1
;
tracer l'allure de l'intensité i
A
(t) du courant qui traverse l'enroulement secondaire du transformateur
d'alimentation.
On donne (Figure 2) le modèle équivalent de Thévenin de la charge (induit du moteur à courant
continu et bobine). On note E la fém du moteur, R
T
la résistance totale du circuit de charge du pont
redresseur et L l'inductance totale de l'ensemble moteur et bobine.
Ecrire la relation entre les grandeurs instantanées donnant us en fonction de i, u
L
, et E.
En déduire la relation entre les valeurs moyennes <us> de la tension us et <i> de l'intensité i (on
rappelle qu'en conduction ininterrompue, <us> = (2U
max
.cosδ)/π et on donne R
T
= 2,0 Ω).
Pour <i> = 15 A et E = 211 V, calculer la valeur de l'angle d'amorçage δ.
Le montage fonctionne dans les conditions précédentes.
Compléter le schéma (figure 4), en précisant les polarités si nécessaire ainsi que les grandeurs
caractéristiques (type d'appareil, fonction, mode, calibre utilisé) du matériel utilisé, afin de visualiser à
la fois l'allure de la tension us(t) et l'allure de l'intensité i(t) ;
Mesurer à la fois la valeur moyenne <i> de l'intensité i, la valeur efficace de l'intensité i
A
(non
sinusoïdale) et la valeur efficace de la tension alternative sinusoïdale u
A
Figure 1
Figure 2

M. Dedieu ; Lycée J.Perrin (95) 5
http://maphysiqueappliquee.free.fr