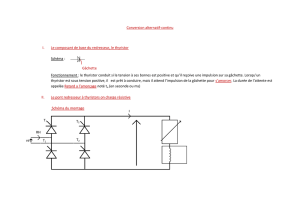
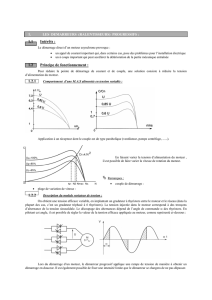
redressement commande

Redressement commandé
Exercice 1
On donne ci-dessous le chronogramme de la tension aux bornes de la charge uC.( 10 V / div ) La fréquence du signal u
issue du transformateur est de 50 Hz. De plus, on donne E = 0,13 n ( n en tr/mn ) et R = 2Ω. Enfin, on supposera le
lissage parfait et i = I = 1 A
1. Déterminer graphiquement l’angle d’amorçage ϑ0.
2. Calculer alors la valeur moyenne de la tension < UC > =
π
MAX
U
( 1 + cos ϑ0 )
3. En déduire alors la vitesse du moteur dans ces conditions
4. Pour quel angle d’amorçage la vitesse est-elle maximale ? Calculer alors cette vitesse nmax
5. Calculer l’angle d’amorçage de démarrage ϑ0 démarrage.
Exercice 2 : BAC 2004
La tension de sortie du transformateur est sinusoïdale de valeur efficace 1200 V
Le courant d'intensité iC absorbé par le moteur ( charge ) est parfaitement lissé ( iC = IC )
L'angle de retard d'amorçage θ0 défini par rapport à la commutation naturelle est égal à θ0 = 30 °
- 1 -
u2
TH1 TH2
D1
D2
iD1
iT1
iM
uc
iC
uL
uM

1. Dessiner sur le doc réponse ci-dessus la forme d'onde de la tension redressée uC
2. Dessiner, en concordance de temps avec la tension précédente, les formes d'onde des courants dans les thyristors
TH1 et dans la diode D1. Vous prendrez soin d'indiquer les intervalles de conduction de chaque interrupteur ainsi
que la nature des phases de fonctionnement ( A : alimentation, RL : roue libre )
3. En déduire l'allure du courant en entrée i ( t ) . Quel type d'appareil doit-on utiliser pour mesurer sa valeur efficace
?
4. On donne l'expression de la valeur moyenne < uC >de la tension uC ( t ) :
< uC > =
max2
U
.
πϑ
0
cos1 +
Comment peut-on la mesurer ?
5. Donner l'expression de la puissance active P absorbée par le moteur en fonction de θ0. Pour quelles valeurs de θ0
cette puissance est-elle maximale ou minimale ?
- 2 -

Exercice 3
On suppose que l’inductance de lissage en série avec l’induit est suffisamment grande pour que le courant dans l’induit
soit parfaitement lissé. On relève les oscillogrammes de grandeurs figurant sur ce schéma
1. Donner le nom des grandeurs représentées : ex y1 = ucharge, …
2. Tracer sur le chronogramme les intervalles de conduction des thyristors
- 3 -
icharge
M
ucharge
v
TH1
TH4
TH3
iT3
iT4
iT1 iT2
i
TH2
Y2
0
ϑ

3. Déterminer graphiquement θ0
4. Indiquer sur les deux schémas de branchement de l'oscilloscope et de la résistance de visualisation RV que l'on
utilise pour relever simultanément v et iT3, puis u et I. L'oscilloscope a une seule voie inverseuse Y1
5. On rappelle que < U > =
π
max2V
. cos θ0 En déduire pour quelles valeurs de θ0 (comprises entre 0 et π ) il y a
fonctionnement :
a. en redresseur
b. en onduleur assisté
Justifier les réponses
6. Quelle relation il y a t_il entre uMOTEUR et < U > ? En déduire une relation entre θ0 et UMOTEUR .
7. Si Veff = 230 V, sachant que n = 14,3 UMOTEUR -143 ( n exprimée en tr/ mn ) , déterminer l'expression numérique de
n en fonction de cos θ0
8. Quelle est la valeur maximale atteinte par UMOTEUR ? En déduire alors nMAX
9. Calculer UMOTEUR au démarrage. Quelle est alors la plage de variation de θ0 pour que le moteur tourne à une
vitesse comprise entre 0 et nMAX ?
- 4 -
ϑ0π + θ0θ
TH1
TH2
TH3
TH4
π2π2π + θ0
icharge
M
ucharge
v
TH1
TH4
TH3
iT3
iT4
iT1 iT2
i
TH2
icharge
M
ucharge
v
TH1
TH4
TH3
iT3
iT4
iT1 iT2
i
TH2

Exercice 4 : BAC 2005
- 5 -