Licence d`Ingénierie Electrique

Contrôle de l’Energie
Février 2004
Durée = 2h Documents non autorisés
L3 SDI EEA
Ingénierie Electrique
Eléments de correction
Exercice 1 : Puissances en alternatif
Soit une charge non linéaire alimentée par une source de tension sinusoïdale de fréquence 50Hz et
d’amplitude 220V qui absorbe un courant alternatif dont la décomposition en série de Fourrier est :
.....)3/t300sin(25,0)8/t200sin(24)6/t100sin(210)t(I
Calculer la puissance active absorbée par cette charge, ainsi que la puissance réactive et apparente.
Comparer les valeurs de S2 et de P2 + Q2. Justifier ce résultat.
P=1905 W, Q=1100 VAR et S=2370 VA. S2 P2 + Q2 à cause puissance déformante (voir cours).
Exercice 2 : Puissances en régime sinusoïdal
Soit une installation électrique constituée d’un moteur à courant alternatif, d’un four, d’un redresseur qui
alimente une machine à courant continu et de 6 lampes à incandescence de 100W chacune, et connectée au
réseau EDF 230V / 50 Hz. On connaît la consommation de chacun des éléments de l’installation :
Moteur : Pmot = 1840W et Imot = 10 A
Four : Pfour = 2875 W et Ifour = 12,5 A
Redresseur : Pred = 2070 W et Ired = 15 A
Calculer la puissance et le courant absorbés par la totalité de l’installation.
Ptotal=7385 W, Qtotal=4140 VAR Itotal=36.8 A et Fp=0.87.
Calculer la valeur du condensateur qu’il faudrait mettre en parallèle avec cette installation pour ramener
son facteur de puissance à l’unité.
C=249uF.
Exercice 3 : Circuit magnétique en continu
Un circuit magnétique, supposé parfait, est constitué par un tore en acier doux de perméabilité relative r =
1590, de section S=10cm2, et de longueur moyenne l=50cm. Ce tore est entouré de n=250 spires d’un
conducteur électrique parcouru par un courant continu i.
1- Calculer les valeurs du champ (B), de l’excitation (H) et du courant i lorsque le flux magnétique
dans le tore est de 0,001 Wb.
B=1T, H=500At/m et i=1A

2- On effectue dans le tore un entrefer de 0,1 cm. Calculez le courant i’ qu’il faut dans le bobinage
pour conserver le flux de 0,001 Wb. Calculer les valeurs de B et H dans les 2 parties du tore
(matériau magnétique et entrefer)
i’=4,18 A Bmat = Bentrefer =1T, Hmat = 500 At/m, Hentrefer =795 103 At/m.
Rappel : La perméabilité de l’air est 0 = 4 10-7 H/m
Exercice 4 : Transformateur en régime sinusoïdal
Un transformateur alimente une installation inductive qui consomme une puissance active de 10kW avec un
facteur de puissance de 0,8 sous 220V / 50Hz. La résistance équivalente des bobinages du transformateur,
ramenée au secondaire, est de 0,1 , l’inductance de fuite ramenée au secondaire est de 0,8 mH.
1- Donnez le schéma électrique du secondaire du transformateur.
2- Calculez le courant au secondaire du transformateur.
I2=56,8A
3- Calculez, en utilisant l’approximation de Kapp (angle entre V20 et V2 faible), la tension secondaire à
vide.
V20=233V.
4- Le primaire est alimenté en 380V. Calculez le rapport de transformation nécessaire pour obtenir la
tension V20 calculée ci-dessus.
k=0,605
5- Lorsque ce transformateur alimenté en 380V fonctionne à vide, il absorbe un courant I10 = 1,7A et
une puissance active P10 = 300W. Calculez le courant et les puissances active et réactive absorbées
par le transformateur lorsqu’il alimente l’installation décrite ci-dessus.
P1=10622 W, Q1=8862VAR I1=36,4 A.
V20
l
r

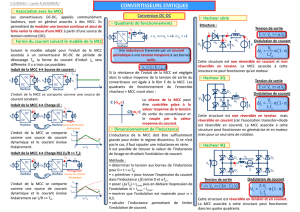
Exercice 5 : Hacheur + Moteur à courant continu (MCC)
On considère le montage de la figure 1, dans lequel K est un interrupteur idéal à 2 positions bidirectionnel
en courant. Cet interrupteur est commandé à une fréquence de 25 kHz, et on désigne par α la « partie » de
la période de commande pendant lequel il est en position 1.
Figure 1 : Schéma du hacheur dévolteur idéal alimentant une MCC
1. En supposant que la tension moyenne aux bornes de la MCC est constante et égale à 100V, indiquez
la valeur de qui permet d’obtenir ce point de fonctionnement.
=1/3.
2. La relation entre la f.e.m de la MCC (E) et sa vitesse ( en rd/s) est donnée par E = 0.3* . La
résistance de l’induit de la MCC, r, est égale à 0.05 . On suppose que le couple de perte de la
MCC est négligeable et quelle entraîne une charge dont la caractéristique couple-vitesse est C =
0.01* . En déduire le courant moyen absorbé par la MCC en régime permanent, lorsque α conserve
la valeur calculer à la question précédente.
Vmmoy=r*Imoy + E avec E = k et Cm = k Imoy. A partir de ces 3 relations, on déduit Imoy=11A.
3. Pour ce même point de fonctionnement de l’ensemble hacheur + MCC, on mesure une ondulation de
courant de 1 A. Donnez la forme d’onde du courant et calculez la valeur de l’inductance L (en
négligeant la résistance r).
Ondulation de I voir cours. Quand K est sur la position 1, di/dt= i/Ton=(300-Vmmoy)/L L=2.6mH.
4. On souhaite modifier le réglage de α pour obtenir une vitesse de la MCC de 30rd/s. Calculez la
valeur de α, le courant absorbé par la MCC et l’ondulation de courant. Donnez la forme d’onde du
courant.
=30rd/s Imoy=1A et Vmmoy=9,05V =0,03
A14,0
LT)1(E
i
.
5. On remplace maintenant l’interrupteur bidirectionnel K par une diode et un transistor. Donnez dans
ce cas le schéma du montage. Les valeurs calculées dans la question précédente sont-elles valables
? Pourquoi ?
Schémas voir cours. Les valeurs calculées en 4 sont valables car, le courant étant toujours positif, le
remplacement de l’interrupteur idéal par des composants non réversibles ne change rien.
K
Induit
MCC
Vo
E
1
2
L
+
r