7.1 Les rappels trigonométriques

La trigonométrie est une des branches les plus anciennes des mathématiques. Les Grecs en avaient fait un outil
efficace pour mesurer des grandeurs que l'on ne pouvait calculer directement, comme la distance d'un navire à
l'horizon, la hauteur d'un monument, etc. Par la suite la trigonométrie ne s'est plus limitée à des rapports entre des
grandeurs géométriques. Elle s'est étendue au domaine des fonctions et a été utile pour représenter des phénomènes
« périodiques ». Avec l'essor de la science moderne, ces phénomènes ont pris une grande importance : vibrations,
ondes, électricité, etc. Aujourd'hui, les fonctions périodiques sont d'une très grande importance en sciences et
forment un domaine majeur des mathématiques.
7.1 Les rappels trigonométriques
Les fonctions trigonométriques sont des fonctions qui, à un angle, associent un nombre. La variable indépendante
est donc un angle qui se mesure par un nombre exprimé dans un système adéquat d?unité. Avant d'étudier les
fonctions trigonométriques, il est nécessaire de rappeler la définition d'un angle, de rappeler les systèmes d'unité
utilisés pour le mesurer et enfin de rappeler les conventions sur sa représentation
7.1.1 Les mesures des angles
Définition:Un angle est la partie du plan comprise entre deux demi-droites issues d'un même point appelé le
« sommet ».
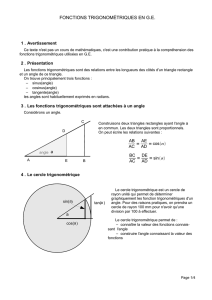
Choisissons d'abord un cercle centré sur le sommet de l'angle. La mesure de cet angle est associée à celle de l'arc
de ce cercle qui est intercepté par les deux côtés de l'angle.
La mesure de l'angle a défini par les demi-droites OA et OP est liée à la mesure de l'arc L intercepté par cet angle
sur le cercle centré à son sommet.Il existe deux systèmes d'unités de mesure pour les angles : les degrés et les
radians.
Définition du degré: La mesure en degrés d'un angle a ou de l'arc de cercle L qu'il intercepte est le rapport de la
longueur L de l'arc de cercle sur la longueur C du cercle multiplié par 360, soit : .
L'angle qui intercepte la circonférence au complet, L = C, s'exprimera en degrés par .
L?origine des degrés remonte à près de trois mille ans, en Mésopotamie. Cette unité découle de la mesure d?une
année, environ 360 jours, un degré équivalant à une journée.
Définition du radian:La mesure en radians d'un angle a ou de l'arc de cercle L qu'il intercepte, est le rapport de la
longueur L de l'arc de cercle sur la longueur du rayon du cercle, soit : ou L = ra.
Pour établir un lien entre les degrés et les radians, nous devons établir un lien entre la mesure a d'un angle en
radians et la mesure b du même angle en degrés. Pour ce faire, utilisons le tour complet. Ainsi
ou , en divisant par 2 l'équivalence.
Les rapports trigonométriques
Chapitre_7:_Les_fonctions_trigonométriques
7.1 Les rappels trigonométriques 1

Le cercle trigonométrique
Nous allons établir une fois pour toutes certaines conventions qui permettront de représenter les angles de la façon
la plus simple possible.
Ces conventions sont les suivantes :
1 Les sommets des angles seront ramenés à l'origine sur un diagramme cartésien;
2 Le premier côté de l'angle coïncidera avec l'axe des x;
3 Le second côté sera obtenu selon le sens positif de rotation, ou sens trigonométrique, c'est-à-dire le sens contraire
des aiguilles d'une montre.
Dans ces conditions, le cercle trigonométrique sera un cercle centré à l'origine et de rayon r = 1. Sur ce cercle, un
angle sera représenté par un seul point : celui où le second côté coupe ce cercle.
Ci-dessous, le point P du cercle trigonométrique indique l'angle de sommet O, de premier côté Ox et de second
côté OP.
7.2 Les fonctions trigonométriques et leur dérivée
Dans cette section, nous allons étudier la dérivée des fonctions trigonométriques
7.2.1 La dérivée de la fonction sinus
Pour calculer la dérivée du sinus, nous aurons besoin des deux résultats:
a)
b)
Démontration de la première limite
La figure ci-dessous représente un angle a sur une partie d'un cercle trigonométrique de rayon r.
Comparons les surfaces des triangles OPH et OMA avec celle du secteur OPA.
Nous avons :
Chapitre_7:_Les_fonctions_trigonométriques
7.2 Les fonctions trigonométriques et leur dérivée 2

7.2.2 La dérivée de la fonction cosinus
Pour calculer la dérivée de y = cos(x), nous allons utiliser la dérivée de y = sin(x) et l'identité trigonométrique
suivante:
7.2.3 La dérivée des autres fonctions trigonométriques
Les dérivées des autres fonctions trigonométriques s'obtiennent en utilisant leurs définitions en fonction de et et les
dérivées de ces deux fonctions que nous venons d'obtenir
Les dérivées des autres fonctions trigonométriques s'obtiennent de façon similaire. Voici les formules, que vous
aurez à retrouver en exercice :
7.3 Les fonctions trigonométriques inverses et leur dérivée
À partir de chacune des fonctions trigonométriques élémentaires, nous allons définir une fonction inverse. Il
faudra, chaque fois, ne prendre que les domaines où la fonction est strictement croissante ou strictement
décroissante pour que son inverse puisse être une fonction, comme nous l'avons vu au chapitre 6. Pour déterminer
ce domaine, nous représenterons graphiquement la fonction et utiliserons le test de l'horizontale pour déterminer un
intervalle où elle est injective.
7.3.1 Les fonctions trigonométriques inverses
La fonction inverse du sinus est appelée l'Arcsinus et se définie comme suit:
y = sin(x) ? x = arcsin(y)
L'inverse de sin(x) ne peut être une fonction que sur un intervalle où la fonction sin(x) est croissante ou
Chapitre_7:_Les_fonctions_trigonométriques
7.3 Les fonctions trigonométriques inverses et leur dérivée 3

décroissante. Voici le graphique de la fonction sin(x):
La fonction est strictement décroissante, donc injective, sur l'intervalle [-Pi/2, Pi/2] et sur cet intervalle, l'image de
la fonction est l'intervalle [-1, 1] .
La fonction inverse aura donc l'intervalle [-1, 1] comme domaine et l'intervalle [-Pi/2, Pi/2] comme image. Pour
obtenir le graphique de y = arcsin(x), on fait une réflexion par rapport à la droite y = x du graphique y = sin(x):
La fonction inverse du cosinus est appelée l'Arccosinus et se définie comme suit:
y = cos(x) ? x = arccos(y)
L'inverse de cos(x) ne peut être une fonction que sur un intervalle où la fonction cos(x) est croissante ou
décroissante. Voici le graphique de la fonction cos(x):
La fonction est strictement décroissante, donc injective, sur l'intervalle [0, Pi] et sur cet intervalle, l'image de la
fonction est l'intervalle [-1, 1] .
La fonction inverse aura donc l'intervalle [-1, 1] comme domaine et l'intervalle [0, Pi] comme image. Pour obtenir
le graphique de y = arccos(x), on fait une réflexion par rapport à la droite y = x du graphique y = cos(x):
L'arctangente est la fonction inverse de la tangente et est obtenue en faisant une réflexion par rapport à la droite y =
x de la fonction y = tan(x) pour x compris entre -Pi/2 et Pi/2.
7.3.2 La dérivée des fonctions trigonométriques inverses
En utilisant le théorème de la dérivée des fonctions composées, nous pouvons généraliser les résultats obtenus aux
fonctions arcsin(u), arccos(u), arctan(u), arcsec(u), arccotan(u) et arccosec(u), avec u une fonction de x.
7.4 Le mouvement harmonique
Un mouvement circulaire est le mouvement d'un point se déplaçant sur un cercle.
Chapitre_7:_Les_fonctions_trigonométriques
7.4 Le mouvement harmonique 4