2. Exploitation.

PARAMETRES INFLUANT SUR
L’ENERGIE TRANSFEREE PAR UN
GENERATEUR AU RESTE DU CIRCUIT
RESISTIF.
Objectifs :
Etudier les paramètres influant sur l’énergie transférée par le générateur au reste du circuit.
Etudier les associations de résistances.
Etablir la loi de Pouillet.
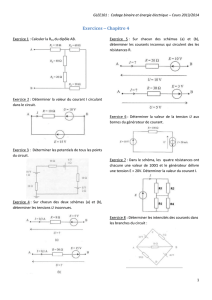
I – Influence de l’agencement de résistances placées aux bornes d’un
générateur de tension continue.
1- Expérience :
On dispose en série 3 résistances de même valeur aux bornes d’un générateur de tension réglé sur 6V.
a) Modifie-t-on l’intensité ou la tension délivrée par le générateur :
- si on modifie le nombre de résistances dans le circuit ?
- si on modifie la disposition des résistances ?
Formulez vos hypothèses et vérifiez les par l’expérience.
b) Pour quelle association la puissance délivrée par le générateur est-elle la plus grande ?
c) De quoi dépend l’énergie transférée par le générateur au circuit ? Conclure.
2- Les résistances équivalentes :
On désigne par Req la résistance unique qui, placée entre A et B, recevrait la même puissance sous
la même tension UAB et le même courant I.
Req est appelée résistance équivalente de l'association des résistances placées entre A et B.
Pour les 2 associations suivantes : Les 3 résistances en série et les 3 résistances en parallèle :
a) Effectuez un bilan des puissances pour chaque association.
b) A partir du bilan des puissances, exprimez Req en fonction des 3 résistances pour chacune des
deux associations.
c) En généralisant, énoncez les lois d'associations des résistances en série ou en parallèle.
TP de Physique n°11
E
R3
UAB
U2
U3
D
I
B
R2
R1
C
A
U1

II – Quelle est la puissance max. disponible aux bornes d’un générateur?
1. Expérience.
Le générateur G étudié est constitué de l'association en série
d'une source de tension E = 6,0 V et d'une résistance
rg = 220 .
Ce générateur fournit la puissance Pe à une résistance R
variable de 0 à 1000 .
Réalisez le montage permettant de relever les variations de P
en fonction de l'intensité I du courant débité par le générateur.
2. Exploitation.
A l'aide du logiciel Winregressi, calculer Pe , puis affichez le graphe de Pe = f(I).
U (V)
I (A)
a) Quel est le bilan énergétique du générateur ? Pe
a.1) Modélisez la courbe représentative de Pe = f(I) par une fonction.
a.2) Cette fonction vous permet-elle de retrouver les transferts d'énergie
au niveau du générateur ?
I
b) Quelle est la puissance maximale disponible aux bornes du générateur ?
b.1) Pour quelle valeur de I le transfert d'énergie entre le générateur et la résistance R est-il maximal ?
b.2) Proposez une méthode de détermination de la valeur de R correspondant à cette situation.
b.3) Pour quelles valeurs de I le transfert d'énergie entre le générateur et la résistance R est-il nul ?
b.4) A quelles situations particulières correspondent ces deux valeurs ?
Laquelle de ces deux situations est-elle périlleuse pour le générateur et pourquoi ?
c) Quel est le bilan énergétique du circuit ?
c.1) Effectuez le bilan des puissances pour l'ensemble du circuit.
En déduire la relation exprimant I en fonction de E, rg et R.
c.2) Généralisation de cette relation :
Pour un circuit entièrement résistif, l’intensité I du circuit délivrée par le générateur de f.e.m. et de résistance
équivalent Req est donnée par la relation :
IE
Req
: c'est la loi de Pouillet qui permet de prévoir le
comportement du circuit. ( à savoir retrouver)
Que représente Req dans cette expression ?
c.3) Retrouver la valeur de R permettant de disposer d'une puissance maximale aux bornes du générateur.
E
rg
R
A
B
(G)
P
N