Faculté des Sciences de Tétouan

Faculté des Sciences de Tétouan
Master Mécatronique 1 Actionneurs électriques J Diouri
Test 1/Enoncé et corrigé
7 mai 2012, durée 2H
Exercice 1
On rappelle dans la figure ci-dessous le schéma équivalent simplifié d’un transformateur en charge.
On considère un transformateur monophasé 220V/110V-50Hz de puissance apparente 1100 VA.
On a procédé aux essais expérimentaux qui ont donné les valeurs suivantes :
– essai à vide : V1 = 220 V, I1v= 260 mA, PV = 25W;
– essai en court-circuit (au secondaire) : I2CC = 10 A, V1CC = 6,22 V ;
– résistances primaire et secondaire mesurées à chaud :
 12.0 ; 4.0 21 RR
1. Tracer le circuit simplifié pour chaque essai
2. Calculer les éléments de la branche en dérivation.
3. Calculer l’impédance totale ramenée au secondaire
sss jLRZ 
4. Calculer la chute de tension
2
0
2VVV 
obtenue lorsque V1 = 220 V et que le transformateur débite au
secondaire un courant inductif I2 = 10 A avec
8.0cos 2
.
Corrigé
2. Dans l’essai à vide, le schéma se réduit à la seule branche en dérivation alimentée par V1. On en tire :
 1936
25
2202
2
1FV R
R
V
P
HLLVARPSQ
L
V
Qvv 3
100
940
9404,5125)220*26,0( avec 11
2222
1
2
1
3.
 22,0
4
1
2
2
1
2R
R
k
R
RRs
. D’autre part, le schéma de l’essai en CC se ramène à Zs alimentée
par
V
Vcc 11,3
2
1
et parcourue par
AI cc 10
2
, d’où l’impédance
 311,0
10
11,3
s
Z
et par conséquent :
 22,0
22 sss RZL
4. La chute de tension est donnée par la formule approchée de Kapp
VILRV ss 1,310)6,0.22,08,0.22,0()sincos( 222 
Exercice 2

3. On veut calculer l’énergie magnétique
m
W
nécessaire pour produire un flux dans le circuit. On rappelle
la formule :
IddWm
. En se servant de la relation de définition de L (liant à I), établir l’expression de
m
W
en fonction de , N, I et des dimensions du circuit.
En déduire par dérivation l’expression de la force f qui agit sur la tige d’abord en fonction de puis en
fonction de I.
Corrigé
1. cours. Condition : circuit linéaire, perméabilité définie constante.
2. la réluctance du fer est négligeable, il reste les 2 entrefers en série :
S
gx
S
g
S
x
000
et
l’inductance
gx SN
N
L
2
0
2
3.
L
d
IddWm
d’où
SN
x
W
f
SNgx
L
Wm
m2
0
2
2
2
0
222
2
1
ou, en remplaçant par
LI
, on trouve l’expression donnée :
2
2
0
2
)(
2xg
SN
I
f
Applications possibles : bras de capture, relais, fermeture/ouverture de circuit à distance..
Exercice 3
La figure montre le schéma d’une ligne alimentant un gros moteur de puissance (5000x736=3680 kW)
Calculez :
La puissance réactive et active consommées par le moteur dans les conditions de fonctionnement indiquées sur
la figure (Rép. 2720 kW ; 1696 kVAR)
La figure ci-contre représente un actionneur
électromagnétique. La tige du milieu est la partie mobile. Elle
glisse sans frottements dans un mouvement horizontal. Sa
position est repérée par l’abscisse x. On note S la section de la
tige et on suppose qu’elle est égale à la surface utile de
l’entrefer qui a une épaisseur g. Les spires sont parcourues
par un courant constant I.
1. Démontrer la relation
S
l
qui donne la réluctance
d’un circuit magnétique. Quelles sont les conditions
d’application de cette relation ?
2. Exprimez en fonction des données, la réluctance totale du
circuit magnétique ainsi constitué. En déduire l’expression
de l’inductance L du circuit.

La puissance réactive fournie par la ligne (Rép. 796 kVAR)
Le courant tiré par la ligne (Rép. 409 A)
Le facteur de puissance de la ligne (Rép. 96%)
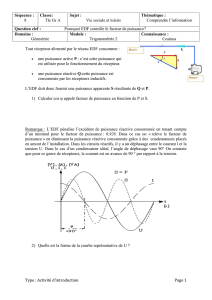
Tracez le diagramme vectoriel de la ligne en précisant les valeurs numériques des angles entre les différentes
grandeurs.
Corrigé
Puissance apparente consommée par le moteur :
kVAS 3200462.40003 
Puissance active consommée :
kWSP 272085,0.3200cos 
Puissance réactive consommée :
kVARSQ 169653,0.3200sin 
La puissance réactive fournie par la ligne
kVARQQQ Cmot 7969001696 
Courant tiré par la ligne :
AIkVAQPUISl409
3.4000
2834
2834322 
Facteur de puissance de la ligne :
%96cos  S
P
Diagramme
I2=462A
Il=409A
IC
V2
2
1