Système à deux miroirs sphériques coaxiaux : télescope

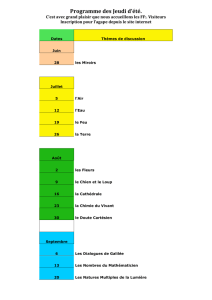
Système à deux miroirs sphériques coaxiaux : télescope Cassegrain.
Un système optique est constitué de deux miroirs sphériques, à faces réfléchissantes en regard : l'un
M1 concave, de rayon R1, et percé d'une petite ouverture centrée sur son sommet S1, l'autre
M2, convexe, de rayon R2, de sommet S2, et de même axe que M. On se placera dans le cadre de
l'approximation de Gauss. Les rayons sont ici des grandeurs positives.
A. Les miroirs M1 et M2, sont coaxiaux mais non concentriques.
(Télescope Cassegrain).
1. On dirige l'axe commun du système vers le centre d'un astre de faible diamètre apparent de
façon que la lumière se réfléchisse d'abord sur M1, puis sur M2. Le système ayant un
encombrement imposé (
12 4 mS S a
), on désire que l'image finale se forme dans le plan
de front de S1 et soit = 5 fois plus grande que celle que donneraient le miroir M1 seul.
Déterminer les rayons R1 et R2 que doivent avoir chacun des miroirs.
2. Déterminer la position du foyer objet F de ce système : on exprimera
1
SF
en fonction de a,
R1 et R2.
B. Les miroirs M1 et M2 sont concentriques (même centre O).
Ce système donne d'un objet ponctuel A, placé sur l'axe
12
SS
une image définitive A' après une
réflexion sur M1 et une réflexion sur M2.
3. Etablir la relation de conjugaison qui lie
et ' 'p OA p OA
.
4. Exprimer le grandissement du système en fonction de p et p'.
5. Calculer la distance focale
'f
du système optique équivalent à M1 et M2.
6. On donne l'encombrement
12
SS
= a = 4 m et le rayon R1 = 8,7 m. Calculer l'abscisse
OA
d'un petit objet lumineux AB pour que l'image A'B' se forme dans le plan de front de
1
S
: déterminer alors le grandissement du système.
www.kholaweb.com