Lesfari, A. : Le théorème de Sard.

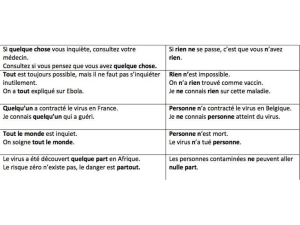
A⊂Rmε > 0
εRm\A
RmM m B ⊂M
M(U, ψ)M ψ(A∩B)
Rm
M N ϕ :M−→ N
x∈M ϕ
dϕx:Tx−→ Tϕ(x),
dim M ϕ
x C ⊂M
ϕ ϕ(C)ϕ
N\ϕ(C)ϕ
dim M < dim N M ϕ
ϕ(M)
ϕ(C)
C
ϕ:M−→ N C
ϕ(C)ϕ
N N\ϕ(C)
N

(Uj, ψj)MUj
M j ϕ(Uj)
N j
ϕ(C∩ Uj)
M=URmN=Rn
m m = 0
C≡C0ϕ
Ck=½x∈ U :∂αϕ(x)
∂xα= 0,∀α∈Nm|α| ≤ k¾, k ∈N∗
C≡C0⊃C1⊃C2⊃ ··· ⊃ Ck⊃Ck+1 ⊃ ···
ϕ(Ck\Ck+1)
(i)ϕ(C0\C1)ξ∈C0\C1
ϕ1, ..., ϕnϕ ξ /∈C1
1ϕ ξ
∂ϕ1
∂x1(ξ)
f:U −→ Rm,(x1, ..., xm)7−→ (ϕ1(x1, ..., xm), x2, ..., xm),
m ξ
VξUf
V W ≡ f(V)f(ξ)RmC0\C1
Vϕ
g≡ϕ◦f−1:W −→ Rn,
U W gWRn
g ϕ V
C0g f(V ∩C)g(C0) =
ϕ(V ∩C)g prRk
Rk
prRn.ϕ =prRm(t, x2, ..., xm)∈ W
g g(t, x2, ..., xm)t×Rn−1
t
gt:¡t×Rm−1¢∩ W −→ t×Rn−1,
g
det µ∂gi
∂xj¶= det µ∂(gt)i ∂xj¶,

µ∂gi
∂xj¶=Ã1 0
?∂gt
i
∂xj!,
g t ×Rm−1
gtg
gt
t×Rn−1g(C0)∩
(t×Rn−1)t∈R
g(C0)
(ii)k≥1ϕ(Ck\Ck+1)
ξ∈Ck\Ck+1
v j ϕ ξ
v(ξ) = 0,∂v
∂xj
(ξ)6= 0.
j= 1
f:U −→ Rm,(x1, ..., xm)←→ (v(x1, ..., xm), x2, ..., xm),
m ξ f
VξU W
(0, ξ2, ..., ξm)Rmf(Ck∩ V)f
v(ξ) = 0 f Ck∩ V 0×Rm−1
g≡ϕ◦f−1:W −→ Rn,
gr:¡0×Rm−1¢∩ W −→ Rn.
gr
Rng
grf(Ck∩ V)
gr
k ϕ n
gr◦f(Ck∩ V)Rn
ϕ(Ck∩V)Ck\Ck+1
Vϕ(Ck\Ck+1)

(iii)ϕ(Ck)k
k > m
n−1K d
UCk
ϕ(ξ+h) = ϕ(ξ) + R(ξ, h),
kR(ξ, h)k ≤ αkhkk+1,(α= )
ξ∈Ck∩K ξ +h∈K
K l d
l
K lmd
l
dm
lmK1
ξ∈Ckξ+h∈K1
khk ≤ √md
lϕ(K1)
β
lk+1 β≡2α(√md)k+1 ϕ(ξ)Rnϕ(Ck∩K)
lmV
V≤lmµβ
lk+1 ¶n
=βnlm−n(k+1).
k+ 1 >m
nd→ ∞ V0
N\ϕ(C)
N
N\ϕ(C)N
∅ 6= Ω ⊂N
NΩ ∆ Rp
∆ Ω
ϕ
¤
f:R→R
ϕ(x) = ½e−1
x2x > 0
0x≤0
ϕ]−∞,0]
ϕ{0}