Université Cadi Ayyad Département de physique appliquée FST

Université Cadi Ayyad Département de physique appliquée
FST Guéliz Marrakech 2010-2011
Devoir surveillé N°1
Module : Electromagnétisme Optique (Durée 2heures)
Exercice 1
Soit une coquille sphèrique de rayon interne R1 et de rayon externe R2 remplie par un diélectrique
LHI de constante diélectrique . Le diélectrique contient aussi une densité de charge libre
.0
1) Déterminer les vecteurs D, E et P en tout points de l’espace.
2) Déterminer les charges de polarisations partout où elles existent.
3) En déduire la somme des charges de polarisation.
Exercice 2
Soient E0, B0, k et quatre paramètres donnés. On considère les couples de champs vectoriels
suivants :
)cos(
0
0
),(
0
1
tkxE
trEa
tkxB
tr
cos(
0
0
),(
0
1
B
)cos(
0
0
),(
0
2
tkxE
trEb
0
)cos(
0
),( 0
2tkxBtr
B
1) Montrer que le couple (E1, B1) ne peut pas être un couple de champ
électromagnétique ?
2) le couple (E2, B2) peut-il être un couple de champ électromagnétique ?
3) Si oui, à quelles conditions ? Déterminer alors les distributions de charges
)(t
et
)(tj
sources de ces champs.
4) a) Que devient l’expression de ces sources dans le cas ou :
00
k
.
b) Déterminer alors le vecteur de Poynting ainsi que sa valeur moyenne temporelle.

Exercice 3
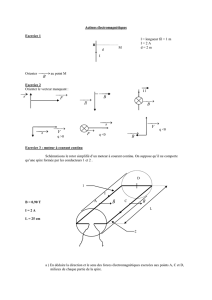
On considère une spire conductrice circulaire C indéformable et fixe, de centre O et de rayon
, de resistance R. Un aimant permanent que l’on assimilera à un dipôle magnétique
m
, se
déplace sur l’axe Oz de la spire. Cet aimant est animé d’un mouvement rectiligne uniforme de
vitesse
k
dt
dz
v
0
. Dans la phase d’approche de la spire, l’aimant se présente le pôle nord en
avant comme indiqué sur le schéma ci-dessous.
1. Préciser, à l’aide d’un schéma en justifiant votre choix, le sens du courant dans les deux cas
suivants : a) On éloigne l’aimant de la spire. b) On approche l’aimant de la spire.
2. Le champ magnétique en un point M de la spire dérive du potentiel vecteur
2
0
4
)( r
em
MA r
( r = PM ,
PM
PM
er
)
Exprimer le champ électromoteur en tout point de la spire.
3. En déduire l’expression de la force électromotrice puis celle du courant i(t) qui
apparraissent dans la spire.
4. Dans quelle position de l’aimant le courant induit est-il maximal.
5. Tracer l’allure de variation du courant i = f(t) et commenter la courbe obtenue.
On donne
Expression du divergence en coordonnées sphériques :
rAr
r
rAdiv  )(1 )( 2
2