Modèle mathématique. Ne pas hésiter à consulter le fichier d`aide

Rappels de géométrie collège
1) droites remarquables d’un triangle
 Médianes : droites qui passent par un sommet et le milieu du côté opposé
Les 3 médianes se coupent au centre de gravité du triangle
CG =
Error!
CC' ou C'G =
Error!
CC' ou CG = 2 C'G
 Hauteurs : droites passant par un sommet et perpendiculaires au
côté opposé
Les 3 hauteurs se coupent à l'orthocentre du triangle.
L'aire du triangle est
A =
Error!
BC × AH =
Error!
BK × AC =
Error!
AB × LC = (
Error!
base × hauteur)
 Médiatrices : droites perpendiculaires à un segment en son milieu
Les trois médiatrices se coupent au centre du cercle circonscrit au triangle
OA = OB = OC
propriété caractéristique : Un point M est sur la médiatrice d'un segment si et seulement si il est équidistant des
extrémités de ce segment.
 Bissectrices : droites coupant un angle en deux angles égaux
Les trois bissectrices se coupent au centre du cercle inscrit au triangle, c'est à dire le cercle
tangent aux 3 côtés du triangle.
2) Triangles rectangles
 Théorème de l'angle droit :
Si AMB est inscrit dans le cercle de diamètre [AB ] alors le triangle AMB est rectangle en M
Etant donné un cercle de diamètre [AB], pour tout point M de ce cercle ( M A et M B), le
triangle AMB est rectangle en M.
 Théorème réciproque au précédent :
Si un triangle est rectangle, alors il est inscrit dans le cercle ayant pour diamètre son
hypoténuse (autrement dit son cercle circonscrit à pour centre le milieu de l'hypoténuse).
 Théorème de Pythagore et réciproque :
Le triangle ABC est rectangle en A le triangle ABC vérifie l'égalité : BC² = AB² + AC².
 Trigonométrie dans le triangle rectangle
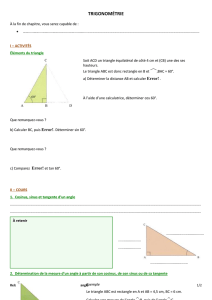
Si ABC est un triangle rectangle en B,
cos( ;A) =
Error!
=
Error!
sin(
Error!
) =
Error!
=
Error!
tan( ;A) =
Error!
=
Error!
formule magique : sohcahtoa !!!
3) Quadrilatères
a) parallélogrammes:
Les quatre propriétés suivantes sont équivalentes :
(i) : Le quadrilatère ABCD est un parallélogramme.
(ii) : Les segments [AC] et [BD] ont le même milieu.
(iii) : AB = CD et AD = BC.
(iv) : (AB) // (CD) et AB = CD.

b) rectangles :
Les trois propriétés suivantes sont équivalentes :
(i) : Le quadrilatère ABCD est un rectangle.
(ii) : ABCD est un parallélogramme et ses diagonales vérifient AC = BD.
(iii) : ABCD est un parallélogramme qui a un angle droit.
c) losange :
Les trois propriétés suivantes sont équivalentes :
(iv) : Le quadrilatère ABCD est un losange.
(v) : ABCD est un parallélogramme et ses diagonales vérifient (AC) (BD).
(vi) : ABCD est un parallélogramme qui a deux côtés consécutifs égaux.
d) carré :
Un quadrilatère est un carré si et seulement si c'est en même temps un losange et un rectangle.
4) Angles
a) quelques rappels utiles :
Angles supplémentaires : ..............................................................................................
Angles opposés par le sommets : ..................................................................................
Angles correspondants : ................................................................................................
Angles alternes-externes : .............................................................................................
Angles alternes-internes : .............................................................................................
Deux angles opposés par le sommet ( respectivement correspondants, alternes-
externes ou alternes-internes) ont même mesure.
b) Théorème de l'angle inscrit
Dans un cercle, un angle inscrit est égal à la moitié de l'angle au centre qui intercepte le
même arc.
Sur la figure ci-contre, ;AMB =
Error!
Error!
.
Conséquence : Deux angles inscrits dans un cercle qui interceptent le même arc sont égaux.
5) Théorème de Thalès
a) Théorème direct
Si A, B et E sont alignés. A, C et F aussi et les droites (BC) et (EF) sont parallèles
alors les quotients
Error!
=
Error!
=
Error!
.
b) Théorème réciproque
Si A, B et E sont alignés dans le même ordre que A, C et F et
Error!
=
Error!
alors les droites (BC) et (EF) sont parallèles.
c) cas particulier : théorème des milieux
 Théorèmes de la droite des milieux :
- La droite joignant les milieux de deux côtés d'un triangle est parallèle au 3ème côté du triangle. De
plus IJ =
Error!
BC
- Si une droite passe par le milieu du côté d'un triangle et est parallèle à un deuxième côté, alors elle
coupe le troisième côté en son milieu.