2008-2009 Sadiki

Collège Sadiki
Devoir de contrôle n° : 3
Sciences physiques
Mercredi :26-4-2008
 On donnera l’expression littérale avant de passer à
l’application numérique.
 L’utilisation de la calculatrice non programmable est autorisée.
 Numéroter les questions.
3ème Maths et Sc.Exp
Profs :Obey- -Cherchari
Durée : 2 heures
Chimie ( 7 points )
Exercice : 1 ( 4,5 pts)
On étudie expérimentalement la réaction d’estérification de l’acide méthanoïque par l’éthanol.
On prépare dans un ballon un mélange équimolaire d’acide méthanoïque et d’éthanol auquel on ajoute
quelques gouttes d’acide sulfurique.
nester(mol)
A une date t=0, ce ballon est placé dans un
bain marie porté à 80°C.
1°/ Ecrire l’équation de la réaction
2°/En cours de réaction, à intervalles de temps
0,066
réguliers, on a prélevé dans le mélange
réactionnel de très petits échantillons de
volume connu, que l’on a dosé avec une
solution d’hydroxyde de sodium de
concentration Cb =2mol.L-1 en présence de
Fig 1
phénolphtaléine(..) . On peut ainsi connaître
l’évolution du mélange réactionnel au cours du
temps. A l’aide de cette expérience on a pu
t(min)
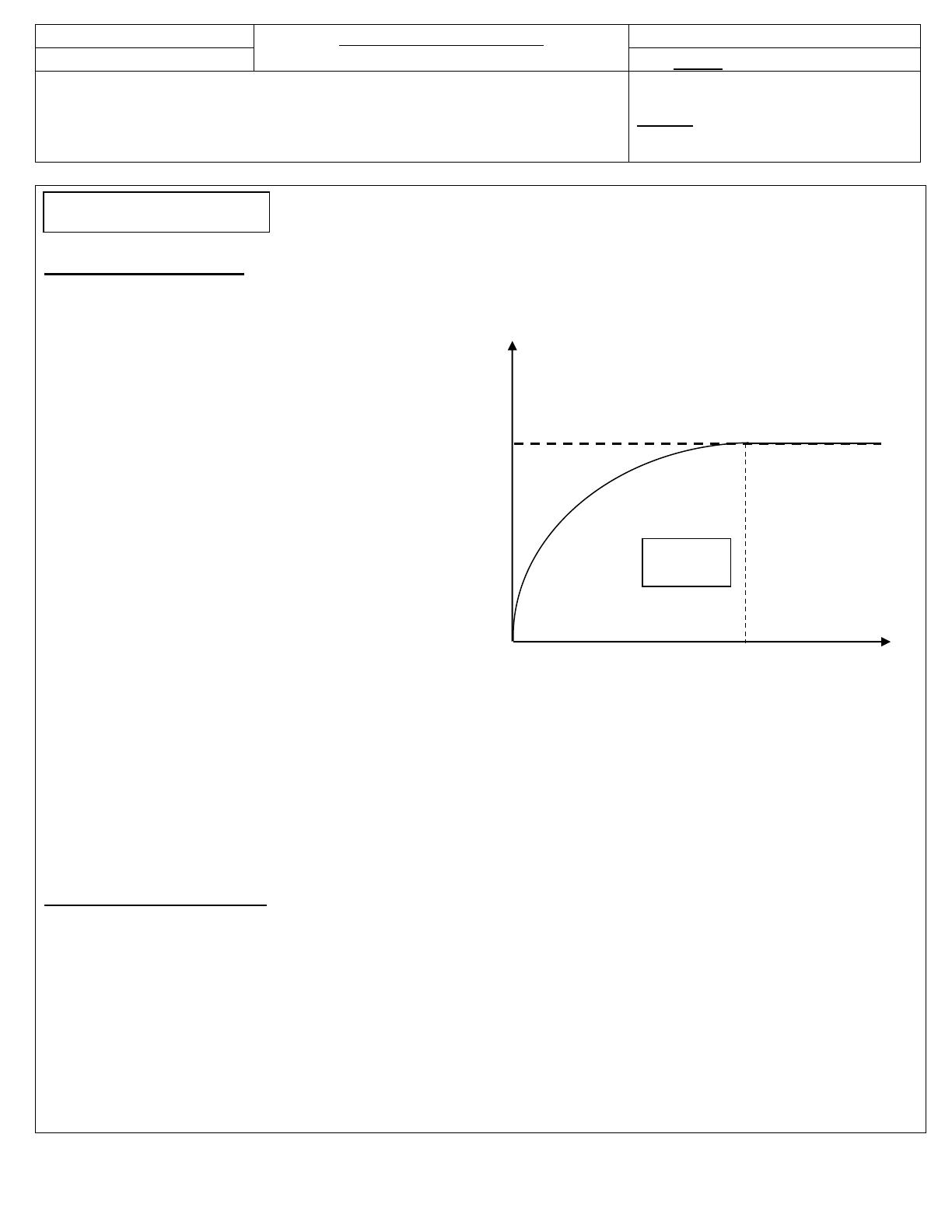
représenter la courbe de variation du nombre
o
de mole d’ester au cours du temps.(fig 1)
t1
a- Pour quelle raison a- t –on chauffé le
mélange réactionnel ?
b- Pour quelle raison a- t –on refroidi le mélange réactionnel avant de procéder au dosage ?
c- Comment peut-on détecter expérimentalement la fin du dosage ?
d- Donner les caractères de cette réaction.
3°/ A partir d’une date t1, tous les prélèvements effectués et dosés ont montré que le volume de base
versé à l’équivalence ne varie pas et qu’il est égal à 17 mL.
a- Dans quel état se trouve la réaction chimique à partir de la date t1 ? Expliquer.
b- Déterminer la composition du mélange réactionnel à partir de cette date. Déduire la composition
initiale du mélange.
Exercice n : 2 ( 2,5 pts )
On dissout une masse m= 1,10 g d’un acide A dans l’eau pure afin de préparer une solution (S) de
volume V=100 mL et de concentration molaire C. On prélève 20mL de la solution (S) que l’on fait
réagir avec un excès de fer.
1/ Ecrire l’équation de la réaction.
2/ - Le volume total du gaz dégagé au cours de cette réaction est VG= 30 mL,
a- calculer la concentration molaire C. On donne VM=24 L.mol-1 volume molaire.
b- calculer la masse molaire de l’acide. Déduire sa formule brute.
c- Ecrire la formule semi développée et le nom de chaque isomère de A.
1
(P)
Physique ( 13 points )
(C2)
Exercice 1 (7 pts) : ( On prendra g = 10 m.s-2.)
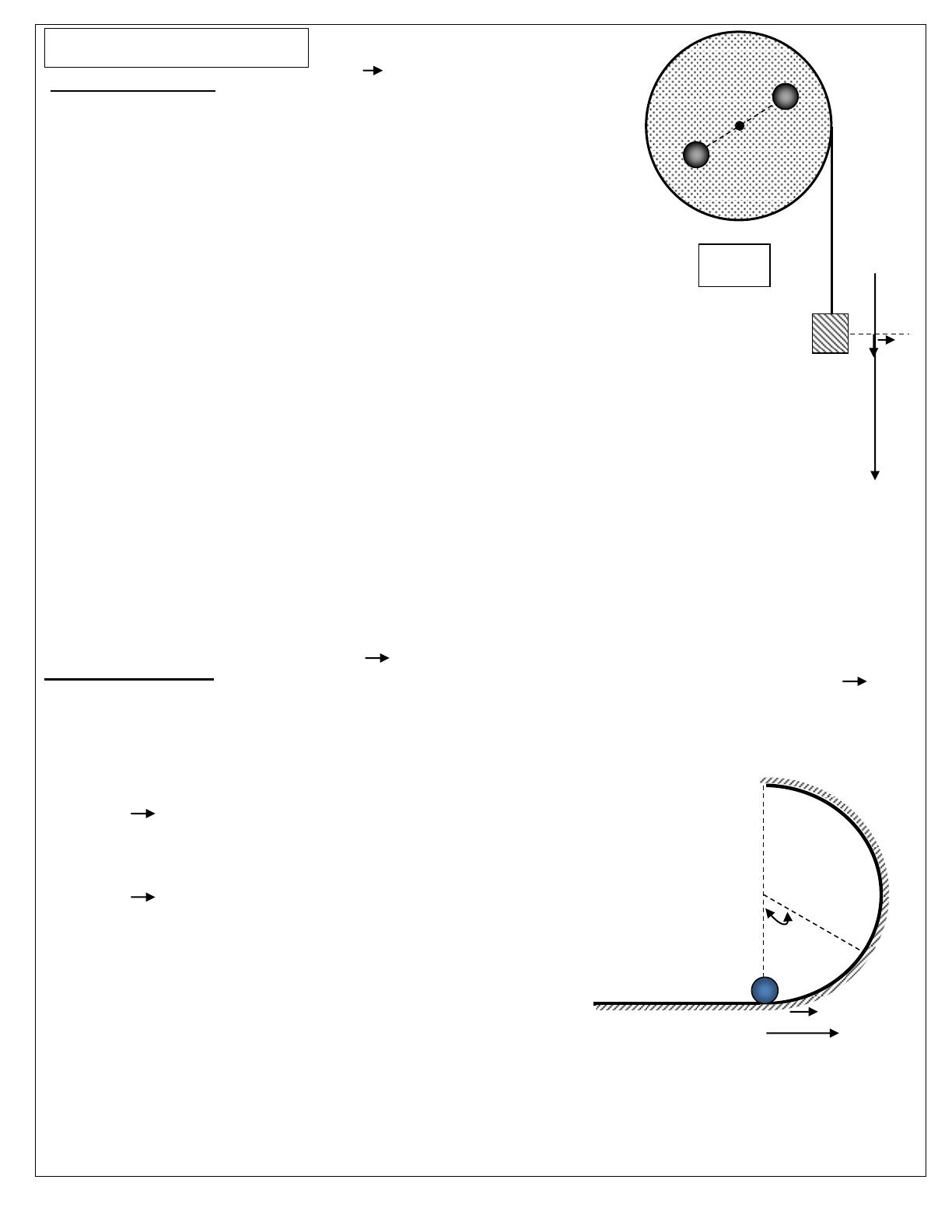
Une poulie (P) pleine, de rayon R=0,5 m, de masse m=1 Kg, peut
B
()

tourner sans frottement autour d’un axe () confondu avec son axe de
O
A
symétrie. Sur l’une de ses faces verticales de centre O, il porte deux
surcharges ponctuelles de même masse m’=mA=mB=2Kg ; ces
surcharges sont situées sur un diamètre en deux points A et B
symétriques par rapport à O tel que OA=OB=R/2. Un fil inextensible
de masse négligeable est entouré par l’une de ses extrémité sur la
Fig 2
poulie et porte à l’autre extrémité un solide (S) de masse M=0,5
Kg.(Voir figure 2)
1- Le moment d’inertie de la poulie seule par rapport à l’axe ()
O
est J0=Error!.
S
i
a- Etablir l’expression du moment d’inertie J par rapport à (), du
système S0 ={poulie + surcharges A et B} en fonction de
m, m’ et R.
b- Montrer que J=0,375 Kg.m2.
2- A l’origine des dates, le système est abandonné sans vitesse
initiale.
x
a- A l’aide d’une étude dynamique, établir l’expression de
l’accélération du solide (S). Quelle est la nature de son mouvement.
b- Calculer l’accélération angulaire ’’ du système S0.
3- Lorsque le solide (S) a effectué un déplacement x=6,28 m, le fil se détache de la poulie.
a- Calculer, à cette date, la vitesse angulaire ’ de rotation de la poulie.
b- Déterminer le nombre de tours effectués par la poulie entre la date t=0 et la date où le fil se
détache de la poulie.
c- Déduire le mouvement ultérieur de la poulie.
Exercice 2 (6 pts) : ( On prendra g = 10 m.s-2.)
Un solide S ponctuel de masse m=1g est lancé à partir d’un point A avec une vitesse V0 sur
une glissière circulaire de centre O et de rayon r. On suppose que les frottements sont négligeables et la


position du solide sur la glissière est repérée par l’angle  =( ;OA ;OM) (OA est vertical).
1- En appliquant le théorème de l’énergie cinétique,
B
exprimer la vitesse V du solide au point M en fonction de
V0, g, r et .
2- Par application de la relation fondamentale de la
r
dynamique, établir l’expression de la valeur de la réaction
R exercée par la glissière sur le solide (S) en fonction de
O
m, g, r,  et V0.
3- Pour vérifier ces résultats théoriques, on a réalisé

l’expérience en communiquant au solide une vitesse
M
S
initiale V0 de valeur 0,6 m.s-1, le rayon r=0,2 m, on a
remarqué qu’il atteint avec une vitesse nulle un point M1
A V


0
défini par 1=( ;OA, ; OM) =60°.
a- Calculer :
 Ec : variation d’énergie cinétique du solide entre A et M1.

 W : somme des travaux du poids et de la réaction ;R.
b- Comparer Ec et W. Quelle conclusion peut-on tirer ?
2
3