Clown (enseignant)

1
NIVEAU
1er cycle du secondaire
COMPÉTENCES TRANSVERSALES
D’ordre intellectuel
D’ordre méthodologique
D’ordre personnel
De l’ordre de la communication
1. Exploiter l’information
2. Résoudre des problèmes
3. Exercer son jugement critique
4. Mettre en œuvre sa pensée
créatrice
5. Se donner des méthodes de
travail efficaces
6. Exploiter les T.I.C.
7. Coopérer
8. Actualiser son potentiel
9. Communiquer de façon
appropriée
COMPÉTENCES MATHÉMATIQUES
Résoudre une situation-problème
Raisonner sur des concepts et des processus mathématiques
Communiquer en langage mathématique
CONTENUS MATHÉMATIQUES
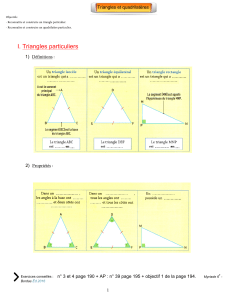
- Figures géométriques : triangles et quadrilatères
o caractéristiques par leurs angles, leurs côtés et leurs diagonales
- Énoncés de géométrie euclidienne
TYPE D’ACTIVITÉS
Exploration Coopération
Manipulation Simulation
Ludique Communication
Situation-problème Projets
INTENTION PÉDAGOGQIUE
Réactiver les connaissances antérieures
Introduire d’une nouvelle notion mathématique
Faire un modelage pour présenter une procédure
Pratiquer avec les pairs
Pratiquer de façon autonome
Consolider une notion
Analyser - Synthétiser (plusieurs notions) – examen synthèse
TYPE DE CONNAISSANCES CIBLÉES
Connaissances déclaratives (lois, notions, concepts, règles, formules), …
Connaissances procédurales (processus, démarche, méthodes, techniques),
Connaissances conditionnelles (transfert, situations-problèmes, problématique)
CONCEPTEURS
Activité conçue par Sylvain Archambault et Anabel VanMoorhem
Commission scolaire de la Rivière-du-Nord
DURÉE DE L’ACTIVITÉ : 1 période de 75 minutes

2
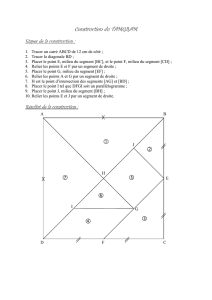
MATÉRIEL ET DÉROULEMENT
Pour un groupe de 32 élèves regroupés en 8 équipes de 4 élèves
- 8 descriptions différentes du clown (chapeau, tête, boutons, bras, etc…), 4 fois. Les membres
d’une même équipe reçoivent la même description, mais ils sont séparés dans la classe.
- 1 feuille réponse à chaque élève
- 8 sacs de type «Ziploc» contenant les 129 figures géométriques (triangles et quadrilatères); 1
sac par équipe
Note : attention au trapèze rectangle ; les élèves ont été portés à croire que c’étaiet un rectangle mal fait. Le sac ne
contient aucun triangle scalène acutangle car l’élève peut confondre avec d’autres types de triangles.
PRÉCISIONS PÉDAGOGIQUES D’APRÈS LES EXPÉRIMENTATIONS
Avant l’activité :
Les élèves connaissent les classifications des quadrilatères et des triangles, selon les caractéristiques des
diagonales, des côtés congrus et des angles opposés chez les quadrilatères.
Pendant l’activité
 distribuer une description à chaque élève en prenant soin de distribuer la même description aux
membres d’une même équipe;
 distribuer une feuille réponse à chaque élève;
 individuellement, les élèves répondent en donnant le nom de la figure géométrique qui représente
chaque aspect du clown : donner environ 10 à 15 minutes pour identifier la figure correspondant à
la description;
 inviter les élèves à déposer leurs crayons, car ils ne devront pas effacer les réponses qu’ils ont déjà
inscrites sur leurs feuilles, puis à se regrouper en équipes;
 en équipe, les élèves valident les descriptions en confrontant leurs réponses, puis utilisent les figures
contenues dans le sac Ziploc pour construire le clown;
 l’enseignant est invité à valider le clown construit par l’équipe, ce qui constitue la partie commune
de l’activité. L’enseignant peut donner une note d’équipe si l’activité est faite en évaluation.
L‘enseignant recueille les feuilles de réponses individuelles pour donner aussi une note individuelle.
Il pourrait aussi en profiter pour évaluer la compétence transversale Coopérer ;
 attribuer 20 à 30 minutes aux élèves pour construire leur clown.
Après l’activité
Retour, par des exercices d’intégration de type «papier-crayon» sur les propriétés des figures
géométriques ou retour en classe sur les stratégies de discussion en équipe, de fonctionnement de
l’équipe.
Construction d’un réseau sur les figures géométriques pour que les élèves puissent voir les points
communs et les points différents des diverses figures géométriques et faire des liens entre les
propriétés.
Note :
Cette activité a été faite comme évaluation sommative sur ce point du programme (068-116). C’est
pourquoi les élèves ne pouvaient changer leurs réponses et étaient invités à déposer leur crayon avant
la discussion en équipe. Les équipes de travail pour la réalisation de cette activité étaient les mêmes
tout au long de l’étape.