Le Portail du Collège Stanislas

1
Exercice 1 (2 points)
On admet que pour tout x appartenant à R , exp( x) Ã x.
Démontrer que : pour tout x  ]0 ; +∞[ , exp(x) –
Error!
à 0 .
Soit la fonction u définie sur Ë par u(x) = exp(x) –
Error!
. Cette fonction est dérivable sur Ë étant une somme de fonctions
dérivables sur Ë et pour tout réel x, u'(x) = ex - x. Cette dérivée est donc positive et la fonction u est croissante sur Ë. Or u(0) = 1,
donc pour tout réel x > 0, u(x)  u(0)  0, ce qui montre que pour tout x de ]0 ; +[, exp(x) –
Error!
 0.
En déduire x + ;lim
Error!
On suppose que x > 0. Il résulte de l'inégalité exp(x) –
Error!
 0 que exp(x) 
Error!
, et, en divisant par x, on obtient:
Error!
Error!
.
Or x +;lim
Error!
= +, ce qui donne par un théorème de comparaison:
Error!
Error!
= +.
________________________________________________________________________________________________________
Exercice 2 (2 points) Q. C. M
(1) L' équation e2x - 3ex - 4 = 0 admet dans R :
a) 0 solution b) 1 solution c) 2 solutions d) plus de 2 solutions
Réponse: b)
(2) L' expression – e-x.
a) n' est jamais négative b) est toujours négative c) n'est négative que si x est positif d) n'est négative que si x est
négatif
Réponse: b)
(3) x  + ;lim
Error!
=
a) -
Error!
b) 1 c) 2 d) + 
Réponse: c)
(4) L' équation différentielle y = 2y ' − 1 a pour ensemble de solutions : ( k désignant une constante réelle)
a.) x  k e 2x+
Error!
b) x  k e 2x –
Error!
c) x  k e 0,5 x – 1 d) x  k e 0,5 x +
1
Réponse: c)
________________________________________________________________________________________________________
Collège Stanislas
Terminale S
Jeudi 27 novembre 2008
Contrôle de mathématiques
Corrigé

2
Exercice 3 ( 6,5 points)
On admet que l’axe des abscisses est
asymptote horizontale à C et à Γ au
voisinage de + .
Partie A
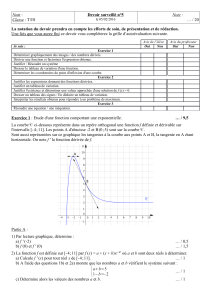
On donne dans un repère orthogonal les courbes C et Γ représentatives de deux fonctions définies et dérivables sur R.
On sait que l’une de ces fonctions est la fonction dérivée de l’autre, on peut donc les noter g et g ′.
1. Associer à chacune des fonctions g et g ′ sa représentation graphique .
On justifiera le résultat en donnant un tableau où figureront le signe de g ′(x) et les variations de g sur R.
C est la courbe représentative d'une fonction positive sur Ë et ne peut pas être la courbe de g', sinon g serait croissante sur Ë, ce qui
est incorrect puisque Γ n'est pas la courbe représentative d'une fonction croissante sur Ë.
La courbe représentative de g est donc C et celle de g' est Γ.
Tableau de variation:
x
-
-1
1
+
g'(x)
-
0
+
0
-
g(x)
+
0
g(1)
0
2. Quel est le coefficient directeur de la tangente à C au point d’abscisse 0 ?
Le coefficient directeur de la tangente à C au point d'abscisse 0 c'est g'(0) = 1.

3
Partie B
Soit l’équation différentielle (E) : y′ + y = 2(x +1) e-x.
1. Montrer que la fonction f0 définie sur R par f0(x) = (x² + 2 x ) e -x est une solution de l’équation (E) sur R
f0 est dérivable sur Ë étant le produit de deux fonctions usuelles dérivables sur Ë.
Pour tout réel x, f0'(x) = (2x+2)e-x + (x²+2x)(-e-x) = (-x²+2)e-x. On en déduit que:
f0'(x) + f0(x) = (-x²+2)e-x + ( x² + 2 x ) e -x = (2+2x)e-x .
Il en résulte que f0 est bien une solution de l'équation (E).
2. Résoudre l’équation différentielle (E′) : y′ + y = 0 sur Ë.
Les solutions de (E') sont définies sur Ë par: x ke-x , où k  Ë.
3. Montrer que f est solution de ( E ) sur Ë si et seulement si ( f – f 0) est solution de ( E’ ) sur Ë.
Pour toute fonction f dérivable sur Ë, on pose: u = f - f0  f = u + f0.
La fonction u est dérivable sur Ë et u' = f ' - f0'.
f est solution de (E) sur Ë  x  Ë, f '(x) + f(x) = 2(x +1) e-x  x  Ë, u'(x) + f0'(x) + u(x) + f0(x) = 2(x +1) e-x.
 x  Ë, u'(x) + u(x) + f0'(x) + f0(x) = 2(x +1) e-x
 x  Ë, u'(x) + u(x) = 0 (car f0'(x) + f0(x) = 2(x +1) e-x puisque f0 est solution de (E))
 u solution de (E') sur Ë .
En déduire, pour x  R, l’expression de f (x) lorsque f est solution de (E).
On vient de voir que f est solution de (E) si et seulement si f-f0 est solution de (E'). f-f0 s'écrit donc:
x  Ë, f(x) - f0(x) = ke-x, ce qui donne f(x) = f0(x) + ke-x = (x² + 2 x ) e -x + ke-x = (x²+2x+k)e-x, k  Ë.
4. Sachant que la fonction g de la partie A est solution de (E), déterminer g (x) pour x  R.
g(x) = (x²+2x+k)e-x, et comme g(0) = 1 (par lecture graphique), on a: k = 1, d'où: g(x) = (x²+2x+1)e-x.
5. Déterminer la solution h de l’équation (E) dont la représentation graphique admet au point d’abscisse 0 une tangente de
coefficient directeur 0.
h(x) = (x²+2x+k)e-x, d'où h'(x) = (2x+2)e-x +(x²+2x+k)(-e-x) = (-x²+2-k)e-x.
On doit avoir h'(0) = 0 ce qui donne: 2-k = 0 d'où k = 2 et par suite h(x) = (x²+2x+2)e-x.
________________________________________________________________________________________________________
Exercice 4 (9,5 points)
Le but de l’exercice est démontrer que l’équation (E) : ex =
Error!
admet une unique solution dans Ë et de construire une suite
qui converge vers cette unique solution.
I. Existence et unicité de la solution
On note f la fonction définie sur Ë par : f (x) = x −e−x .
1. Démonter que x est solution de l’équation (E) si et seulement si f (x) = 0.
x est solution de (E)  x  0 et ex =
Error!
 x  0 et e-x = x ( par inversion de l'égalité)
 x  0 et x - e-x = 0  x  0 et f(x) = 0.
2.L’objectif de cette question est d’étudier le signe de la fonction f
a. Étudier le sens de variations de la fonction f sur Ë.
f est la somme de deux fonctions usuelles dérivables sur Ë, elle est donc dérivable sur Ë.
Pour tout réel x, f '(x) = 1 + e-x. Comme une exponentielle est strictement positive, f '(x) est positive pour tout réel x. Il en résulte
que la fonction f est strictement croissante sur Ë.
b. En déduire que l’équation (E) possède une unique solution sur Ë, notée α.
x -;lim f(x) = - et x +;lim f(x) = + (résultats évidents).
La fonction f est donc continue et strictement croissante sur ]- ; +[ dont l'image est ]- ; +[. Le théorème des valeurs
intermédiaires montre alors que l'équation f(x) = 0 admet une solution unique  sur Ë.
c. Démontrer que α appartient à l’intervalle [
Error!
; 1].
f(
Error!
)  -0,11 et f(1)  0,63. f(
Error!
) et f(1) sont de signes contraires, la solution  de l'équation f(x) = 0 appartient donc à
l'intervalle [
Error!
;1]
d. En déduire le signe de f sur l’intervalle [0 ; α].
f est croissante et s'annule en , elle est donc négative sur [0 ; ].
II. Deuxième approche

4
On note g la fonction définie sur l’intervalle [0 ; 1] par : g (x)=
1
1x
x
e
1. Démontrer que l’équation f (x) = 0 est équivalente à l’équation g (x) = x.
g(x) = x 
1
1x
x
e
= x  1+x = x(1+ex)  1 = xex  e-x = x  x - e-x = 0  f (x) = 0
2. En déduire que α est l’unique réel vérifiant : g (α) = α.
Les équations f (x) = 0 et g(x) = x étant équivalentes, elles ont les mêmes solutions. Or  est la seule solution de l'équation f(x) = 0
elle est donc la seule solution de l'équation g(x) = x.
3. Calculer g ′(x) et en déduire que la fonction g est croissante sur l’intervalle [0 ; α].
La fonction g est dérivable sur Ë étant le quotient de deux fonctions usuelles dérivables sur Ë.
Pour tout réel x, g'(x) =
2
(1 ) (1 )
(1 )
xx
x
e x e
e
=
2
1
(1 )
x
x
xe
e
=
2
()
(1 )
xx
x
e e x
e
=
2
()
(1 )
x
x
f x e
e
.
Comme une exponentielle est strictement positive, g'(x) est du signe de -f(x) sur [0 ; ]. Or f est négative sur [0 ; ] d'après la
partie I, 2. d). Il en résulte que g'(x) est positive sur [0 ; ] ce qui montre que la fonction g est croissante sur [0 ; ].
III. Construction d’une suite de réels ayant pour limite α
On considéra la suite (un) définie par : u0 = 0 et, pour tout entier naturel n, par : un+1 = g(un).
1. Démontrer par récurrence que, pour tout entier naturel n : 0  un  un+1  α.
Pour tout entier naturel n, soit Pn la proposition : 0  un  un+1  α qu'on va démontrer par récurrence.
 Initialisation: u0 = 0 et u1 = g(u0) =
Error!
. Or   [
Error!
; 1] (Partie I, 2. c)) ce qui montre que: 0  u0  u1  α.
 Hérédité: Soit n un entier naturel. On suppose que 0  un  un+1  α . Comme g est croissante sur [0 ; ] d'après la partie II, 3.
alors g(0)  g(un)  g(un+1)  g(α) soit 0  g(0)  un+1  un+2  α car g() = .
La propriété Pn est donc héréditaire.
 Conclusion: étant initialisée et héréditaire la propriété Pn est vraie pour tout entier naturel n.
2. En déduire que la suite (un ) est convergente. On note ℓ sa limite.
La suite (un) est convergente car c'est une suite croissante et majorée par .
3. Justifier l’égalité : g (ℓ)= ℓ. En déduire la valeur de ℓ.
La fonction g est la fonction qui définit la suite récurrente (un) et elle est continue sur l'intervalle fermé [0 ; ] qui contient tous les
termes de la suite. Le théorème du point fixe donne que g (ℓ)= ℓ.
La valeur de ℓ est donc .
4. À l’aide de la calculatrice, déterminer une valeur approchée de u4 arrondie à la sixième décimale.
La calculatrice donne: u4  0,567143.
__________________________________________________________________________________________________