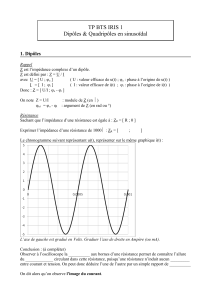
Introduction : Tout phénomène oscillant est sujet à un

1
Introduction :
Tout phénomène oscillant est sujet à un amortissement. Ainsi,
une pendule en oscillation libre finit par s’arrêter en raison des forces
de frottement. Au cours de cet amortissement progressif, le nombre
des oscillations par seconde demeure inchangé, tandis que leur
amplitude diminue peu à peu jusqu’à l’arrêt définitif du pendule. En
électricité, les phénomènes oscillants sont amortis par la résonance
électrique du circuit qui les produit.
But de TP :
On a fait se TP pour Déterminer expérimentalement l’impédance d’un
circuit RLC

2
Partie théorique
Définition :
Un circuit électrique:
Un circuit électrique est un assemblage de différents conducteurs dans
lesquels circule le courant électrique.
Un circuit électrique comporte donc au moins deux éléments : un générateur
(pile, prise du secteur, etc.) et un récepteur (ampoule, moteur, etc.). Les fils de
connexion véhiculent l’énergie électrique du générateur vers le récepteur.
L’interrupteur assure l’ouverture.
Un circuit électrique comporte deux types de conducteurs : des éléments actifs et
des éléments passifs. Les éléments actifs peuvent être des générateurs, définis
par leur force électromotrice (f.é.m.) et l’intensité du courant qu’ils délivrent, ou
bien des récepteurs, tels que les moteurs, caractérisés par une force contre-
électromotrice (f.c.é.m.) et par l’intensité du courant qu’ils consomment (voir
Moteurs électriques et générateurs). Parmi les éléments passifs, on peut
mentionner les résistances, définies par leur résistance R (sachant que tout
conducteur oppose au passage d’un courant une résistance qui dépend du
matériau constitutif et de ses dimensions), les bobines d’induction, définies par
leur inductance L, et les condensateurs, définis par leur capacité C. Lorsque ces
différentes grandeurs sont constantes, le circuit est dit linéaire, car, pour décrire
son comportement, on manipule des équations différentielles linéaires à
coefficients constants.

3
Circuit RLC :
Un circuit dit RLC car il comporte un resistor de résistance R, une bobine
d'auto-inductance L et un condensateur de capacité C de charge initiale q
L’impédance:
Grandeur physique égale au quotient d'une excitation d'un système
physique par la réaction qui en résulte. En électromagnétisme, elle est égale au
quotient d’une tension entre deux points par l’intensité du courant entre ces deux
points.
L’impédance d’un circuit électrique :
La loi d’Ohm peut s’appliquer à un circuit en régime sinusoïdal, mais sous
une forme plus complexe si sont présentes des capacités ou des inductances qui
dépendent du temps. En vue de simplifier les calculs, on introduit alors
l’impédance d’un tel circuit, qui correspond au rapport de l’amplitude de la
tension du circuit à l’amplitude du courant qui le traverse.
L’impédance d’un circuit RLC :
dans un circuit « RLC », associant en série une résistance R, une bobine
d’inductance L et un condensateur de capacité C, l’amplitude I de l’intensité du
circuit est reliée à l’amplitude E de la tension par la relation I = E / Z, où Z se
mesure en ohms.
Z = Z résistance + Z bobine + Z condensateur
D’où :
- Z résistance = R

4
L’impédance d’une résistance parfaite est constante et égale à la valeur de
sa résistance
- Z bobine = L  tel que  = 2 = 2  t Où f est la fréquence du régime sinusoïdal.
et T est la période du régime sinusoïdal.
- Z condensateur = 1 / C  tel que  = 2 = 2  t
L’impédance d’un condensateur parfait dépend de la fréquence du courant
les traversant.
Alors :
Z = R + L j + 1 / C j
 Z = R + j(L  + 1 / C j²)
 Z² = R² + [j(L  -1 / C ) ]²
Donc :
lZl = √R² + (L  -1 / C )²

5
Partie pratique
La manipulation :
 On considère le circuit électrique ci-dessus RLC il comporte un resistor
de résistance R, une bobine d'auto-inductance L et un condensateur de
capacité C de charge initiale q.
 La résistance R étant fixée à R = 200 Ώ ,et la tension en rotation complexe
e = 6V
 VG(t) étant sur la voie 1 de l’oscilloscope et VR(t) sur la voie 2 de
l’oscilloscope
 On ferme l'interrupteur K et on observe les tensions d’entrée VG(t) et
VR(t) en faisant varier la fréquence.
 Les variations décrites dans le tableau suivant :
e(Volt)
(Hz)
t(t)
t=1/(1/t)
=2/t(rd/s)
Φ(t)
Z’
6V
6.25
0.040
0.14
39.25
1.57
3.75
6V
7.12
0.020
0.13
44.71
0.89
2.14
6V
7.68
0.010
0.125
48.23
0.48
1.66
6V
8
0.005
0.117
50.24
0.25
1.25
6V
8.33
0.000
0.116
52.31
0.00
1.15
6V
8.69
0.005
0.114
54.60
0.27
1.25
6V
9.08
0.010
0.113
57.02
0.57
1.50
6V
11
0.020
0.112
62.80
1.25
2.14
6V
11.11
0.030
0.111
69.77
2.09
4.28
On a :
 e Z’ e R*e
 Z’ =    =  d où : I*R= VR  z’ = 
 I R IR VR